Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Исторически единственный шанс решить такие задачи сводился к поиску какого-то хитроумного способа разрезать криволинейную область на полоски или разбить на осколки, а затем пересобрать эти кусочки в уме или взвесить на воображаемых качелях, как это делал Архимед. Однако примерно в 1665 году Ньютон впервые совершил крупный прорыв в решении этой задачи за почти за два тысячелетия. Он объединил идеи исламской алгебры и французской аналитической геометрии, но пошел гораздо дальше.

Согласно его новой системе, первый шаг состоял в том, чтобы отразить нужную область на координатной плоскости и определить уравнение, которое описывает верхнюю кривую, ограничивающую область. Для этого требовалось вычислить, насколько выше оси x расположена эта кривая, то есть для каждого значения x получить соответствующее значение y (как показано на рисунке выше пунктирной линией). Такое вычисление преобразовывало кривую в уравнение, связывающее x и y , что позволяло применять инструменты алгебры. Тридцатью годами ранее Ферма и Декарт уже поняли это и использовали такие методы для поиска касательных к кривым, что само по себе было большим достижением.

Но они упускали из виду тот факт, что сами по себе касательные не так уж важны. Куда важнее угловые коэффициенты , отражающие их наклоны, поскольку именно они привели к понятию производной. Как мы видели в предыдущей главе, производные естественным образом возникают в геометрии как наклоны кривых. Производные также возникают в физике как другой вид изменений, например скорость. Таким образом, производные представляются связующим звеном между наклонами и скоростями и, более широко, между геометрией и движением. Как только идея производной прочно обосновалась в голове Ньютона, ее способность перебросить мост между геометрией и движением привела к окончательному успеху. Именно производная наконец разрешила задачу площади.

Глубоко скрытые связи между этими идеями – наклоны и площади, кривые и функции, скорость изменения и производные – вышли из тени, когда Ньютон взглянул на них с динамической точки зрения. Поразмышляйте над приведенным выше графиком и представьте, что x двигается направо с постоянной скоростью. Вы можете даже думать об x как о времени: Ньютон часто так и делал. По мере движения x площадь серой области непрерывно меняется. Поскольку она зависит от x , ее следует рассматривать как функцию от x , так что запишем ее в виде A ( x ). Когда мы хотим подчеркнуть, что эта площадь является функцией x (в противопоставление фиксированному числу), мы будем называть ее функцией накопления площади , а иногда просто функцией площади .

Мой преподаватель анализа в старших классах, мистер Джоффри, предлагал яркую запоминающуюся метафору для этого «текучего» сценария, когда x скользит, а вместе с ним меняется площадь. Он просил нас представить волшебный малярный валик, который движется по горизонтали. Двигаясь вправо, он окрашивает в серый цвет участок под кривой.

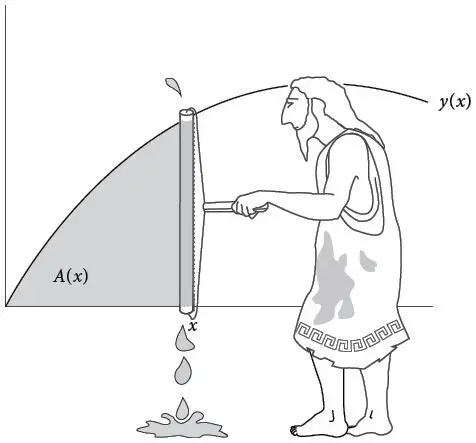
Пунктирная линия в точке x обозначает текущее положение этого воображаемого малярного валика, пока он двигается вправо. При этом для гарантии аккуратного окрашивания валик мгновенно каким-то волшебным образом растягивается или сжимается в вертикальном направлении – в точности от кривой вверху до оси x внизу, но их не пересекая. Волшебство тут в том, что валик при движении всегда меняет свою длину до величины y ( x ), чтобы безукоризненно окрашивать площадь нужной фигуры.

Сочинив такой неправдоподобный сценарий, зададимся вопросом: с какой скоростью серая площадь увеличивается по мере перемещения x вправо? Или, что эквивалентно, с какой скоростью ложится краска, когда малярный валик находится в точке x ? Для ответа на вопрос подумайте, что произойдет в следующий бесконечно малый интервал времени. Валик перемещается вправо на бесконечно малый промежуток dx . Когда он проходит такое крошечное расстояние, его длина в вертикальном направлении практически не меняется, поскольку при столь бесконечно малом перемещении у него почти нет времени на изменение длины (этот тонкий момент мы обсудим в следующей главе). В течение этого короткого интервала валик фактически окрашивает высокий тонкий прямоугольник с высотой y и бесконечно малой шириной dx , бесконечно малая площадь которого равна dA = y dx . Разделив части этого уравнения на dx , мы получим скорость, с которой накапливается площадь. Она определяется соотношением

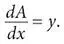
Эта аккуратная формула говорит, что общая окрашенная площадь под кривой увеличивается со скоростью, равной текущей высоте y малярного валика. Это логично: чем длиннее валик в данный момент, тем больше краски он наносит в следующее мгновение и тем быстрее накапливается окрашенная площадь.

Приложив еще немного усилий, мы могли бы доказать, что эта геометрическая версия теоремы эквивалентна версии с движением, которую мы использовали ранее, где утверждалось, что накопленная площадь под кривой скорости равна расстоянию, пройденному двигающимся телом. Однако у нас есть более срочные задачи. Нам нужно понять, что означает эта теорема, почему она так важна и как она в итоге изменила мир.

Следующая диаграмма подытоживает то, что мы только что узнали.

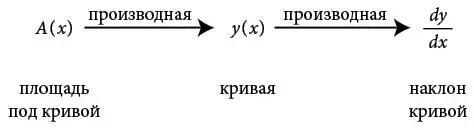
На ней показаны три функции, которые нас интересуют, и взаимосвязи между ними. Наша кривая находится в середине, ее неизвестный наклон – справа, а неизвестная площадь под ней – слева. Как мы видели в главе 6, именно эти три функции фигурируют в трех основных задачах анализа. Имея кривую y , мы пытаемся вычислить ее наклон и площадь.

Надеюсь, эта диаграмма проясняет, почему я назвал поиск наклона «прямой задачей». Чтобы найти наклон для кривой, мы просто следуем по стрелке вправо. Для определения наклона мы вычисляем производную y . Это прямая задача (1), которую мы обсуждали в предыдущей главе.

А вот чего мы не знали прежде, но узнали из основной теоремы сейчас, это то, что площадь A и кривая y тоже связаны производной: основная теорема гласит, что производная A – это y . Это потрясающий факт. Он позволяет нам определить площадь под произвольной кривой, решив тем самым древнюю задачу, почти две тысячи лет ставившую в тупик величайшие умы. Эта картинка подсказывает путь к ответу. Но прежде чем откупоривать шампанское, нужно осознать, что основная теорема дает нам не совсем то, что мы хотим. Она не дает нам непосредственно площадь, но рассказывает, как ее получить.