Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Для сравнения рассмотрим скорость изменений спустя две недели, 15 января. Между этими сутками и следующими продолжительность светового дня возросла на 90 секунд, то есть скорость увеличения составила 1,5 минуты в сутки, что более чем в два раза превышает показатель 0,7 минуты двумя неделями ранее. Таким образом, в январе продолжительность дня не просто увеличивается, а с каждым днем увеличивается все быстрее .

Эта приятная тенденция сохраняется еще несколько недель. С приходом весны дни становятся все длиннее, причем довольно быстро. В день весеннего равноденствия, 20 марта, скорость увеличения достигает восхитительных 2,72 минуты в сутки. Вы можете посмотреть на этот день на графике в главе 4. В этот 79-й день года, то есть примерно после четверти года, день увеличивается наиболее быстро. Это видно на графике – там, где он самый крутой, продолжительность дня растет быстрее всего, то есть производная максимальна – дни удлиняются с максимально возможной скоростью. Все это происходит весной.

Для грустного контраста взгляните на самые короткие дни в году. Здесь двойная печаль: эти мрачные зимние дни не только удручающе коротки, но и меняются крайне медленно, что только добавляет оцепенения. Тем не менее это тоже логично. Самые короткие дни находятся в нижней части синусоиды, отображающей продолжительность дня, а в нижней части волна близка к горизонтальной линии (иначе это не было бы нижней частью – ситуация бы улучшалась или ухудшалась). В силу того что синусоида в нижней части почти горизонтальна, ее производная близка к нулю, а это означает, что скорость изменений стопорится (по крайней мере, на мгновение). В такие дни кажется, что весна не наступит никогда.

Я выделил два времени года, которые имеют большое эмоциональное значение для многих из нас, – период весеннего равноденствия и зимнего солнцестояния, однако не менее поучительно рассмотреть весь год в целом. Чтобы отслеживать сезонные колебания в скорости изменения продолжительности дня, я вычислял их через определенные интервалы времени, начиная с 1 января и далее через каждые две недели. Результаты представлены на следующем графике.

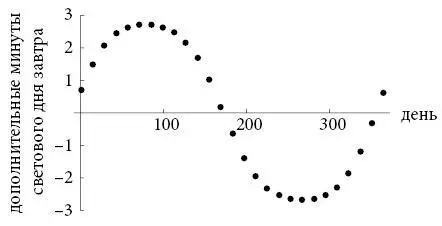
Вертикальная ось отображает ежедневную скорость изменений, то есть количество дополнительных минут светового дня при переходе от одних суток к другим. Горизонтальная ось – пронумерованные дни года, от 1 (1 января) до 365 (31 декабря).

Скорость изменений поднимается и падает, словно волна. Она начинается с положительных величин в конце зимы и начале весны, когда дни становятся длиннее, и достигает пика около 79-го дня (весеннее равноденствие, 20 марта). Как мы уже знаем, именно в это время дни прибывают особенно активно, примерно на 2,72 минуты в сутки. Однако после этого наступает спад. Скорость начинает падать и становится отрицательной после летнего солнцестояния на 172-й день (21 июня). Отрицательной она становится потому, что дни начинают укорачиваться: продолжительность следующего светового дня меньше предыдущего. Скорость достигает минимума примерно 22 сентября, когда день укорачивается сильнее всего, и остается отрицательной (хотя и не такой отрицательной) до зимнего солнцестояния на 355-й день (21 декабря), когда дни снова начинают прибывать, пусть пока и незаметно.

Любопытно сравнить эту волну с той, которую мы видели ранее в главе 4. Если их изобразить на одном графике и поменять масштаб так, чтобы амплитуды были сравнимы, получится следующий рисунок:

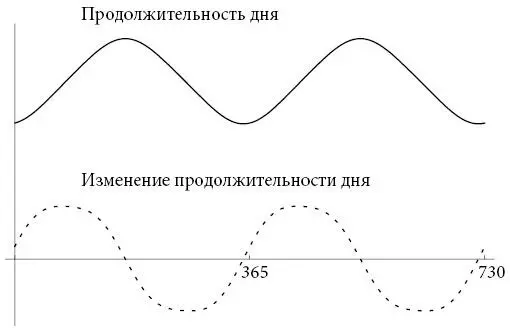
Здесь представлены данные за два года, чтобы подчеркнуть повторяемость волн. А для усиления эффекта сравнения я также соединил точки и убрал числа с вертикальной оси, чтобы сосредоточить внимание на форме волн и зависимости от времени.

Первое, что нужно отметить, – это рассинхронизация волн. Они не достигают пика одновременно. Волна продолжительности дня достигает пика примерно в середине года, тогда как волна скорости ее изменения – примерно тремя месяцами ранее. Если учесть, что каждой волне требуется двенадцать месяцев на полный цикл восходящего и нисходящего движения, то три месяца – это четверть цикла.

Следует также отметить, что волны напоминают друг друга по форме, но с определенными различиями. Несмотря на наличие родственных признаков, пунктирная волна менее симметрична, чем сплошная, а ее пики и впадины более плоские.

Я углубляюсь во все это, поскольку эти волны из реального мира позволяют разглядеть замечательное свойство синусоид: когда некая переменная изменяется по идеальной синусоиде, скорость ее изменений также меняется по идеальной синусоиде со сдвигом на четверть цикла. Это свойство самовоспроизведения характерно для синусоидальных волн. Другие волны им не обладают. Его можно было бы принять даже за определение синусоиды. В этом смысле наши данные намекают на уникальный феномен возрождения, присущий идеальным синусоидам. (Мы еще поговорим об этом в связи с анализом Фурье – мощной областью анализа, благодаря которой появились некоторые наиболее интересные современные применения.)

Теперь я попробую пояснить, откуда берется сдвиг на четверть цикла. Та же самая концепция объясняет, почему при вычислении скорости изменения синусоидальных волн снова получаются синусоидальные волны. Ключевой момент в данном случае заключается в том, что синусоиды связаны с равномерным круговым движением. Вспомните, что, когда точка движется по окружности с постоянной скоростью, ее движение вверх и вниз дает во времени синусоиду. (Впрочем, движение влево и вправо дает то же самое). С учетом всего этого рассмотрим следующую диаграмму:

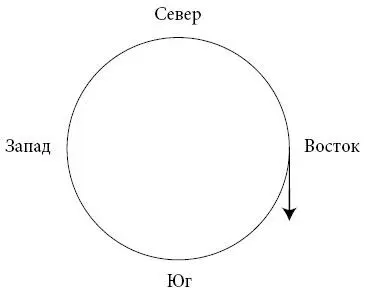
На ней изображена точка, двигающаяся по окружности по часовой стрелке, но эта точка не подразумевает какой-то физический или астрономический объект. Это не Земля, вращающаяся вокруг Солнца, и не что-то связанное с временами года. Просто абстрактная точка, движущаяся по окружности. Ее смещение к востоку (для краткости «восточность») увеличивается и уменьшается подобно синусоиде. Когда точка достигает максимального восточного положения, как на диаграмме, это аналогично максимуму синусоиды или самому длинному дню в году. Вопрос: что происходит дальше, когда точка занимает максимальное восточное положение, а синусоида находится на максимуме восточности? Как видно на диаграмме, в самом восточном положении наша точка направляется на юг , что показано стрелкой вниз. Но юг на компасе находится на 90 градусов от востока, а 90 градусов – это четверть цикла. Эврика! Вот откуда берется сдвиг на четверть цикла. Из-за геометрии окружности всегда существует смещение на четверть цикла между любой синусоидой и волной, полученной из нее в качестве производной, то есть в качестве скорости изменения. В этой аналогии направление движения стрелки подобно скорости изменения. Оно определяет, куда точка пойдет дальше и, следовательно, как она меняет свое положение. Более того, само направление стрелки тоже вращается по кругу, пока точка делает оборот, так что направление стрелки по компасу тоже следует синусоиде. А поскольку направление по компасу подобно скорости изменения – вуаля! – скорость изменения тоже следует синусоидальной закономерности. Это то самое свойство самовосстановления, которое мы пытались понять. Синусоиды порождают синусоиды со сдвигом на 90 градусов. (Специалисты поймут, что я пытаюсь без формул объяснить, почему производная синуса – это косинус, который сам по себе – всего лишь синус, сдвинутый на четверть периода.)