Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

3. Согласно американском закону о людях с ограниченными возможностями, пандусы для инвалидных колясок не могут подниматься круче чем на 1 дюйм на каждые 12 дюймов расстояния по горизонтали. Для пандуса с такой максимально допустимой крутизной отношение между подъемом и горизонтальным участком определяется уравнением y = x / 12, где y – подъем; x – протяженность по горизонтали.

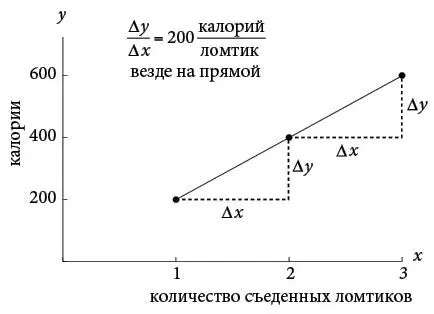
В каждом из этих случаев линейной зависимости зависимая переменная меняется с постоянной скоростью по отношению к независимой переменной. Ставка моей дочери – постоянные 10 долларов в час. Скорость автомобиля – постоянные 60 километров в час. Постоянный наклон пандуса для колясок – 1/12, что определяется как отношение высоты к горизонтальной проекции. То же самое верно для хлеба с изюмом и корицей, который я так люблю: он добавляет в организм калории с постоянной скоростью 200 калорий на ломтик.

На языке анализа скорость изменения (коэффициент) всегда означает частное двух изменений: изменение величины y , деленное на изменение величины x , что символически записывается Δ y / Δ x . Например, если я съем еще два ломтика хлеба, я наберу еще 400 калорий. Поэтому соответствующий коэффициент равен:

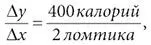
что дает 200 калорий на ломтик. Ничего удивительного. Но следует заметить, что этот коэффициент – константа. Он всегда одинаков, сколько бы ломтиков хлеба я ни съел.

Когда какой-то коэффициент постоянен, заманчиво считать его просто числом , как 200 калорий на ломтик, или 10 долларов в час, или уклон в 1/12. В данном случае это не нанесет вреда, но впоследствии приведет к проблемам. В более сложных случаях этот коэффициент не будет постоянным. Например, представьте себе прогулку по холмистой местности, где одни участки крутые, а другие более пологие. Теперь уклон – это функция вашего местоположения. Было бы ошибочно думать о нем просто как о числе. Точно так же, когда автомобиль ускоряется или когда планета обращается вокруг Солнца, их скорости обязательно изменяются. Поэтому крайне важно рассматривать их как функцию времени. Так что нам нужно сразу приобретать эту привычку. Надо прекратить думать о скорости изменений как о числах. Эти коэффициенты – на самом деле функции .

Потенциальная путаница возможна, когда эти функции – константы, как в случае рассмотренной линейной взаимосвязи. Вот почему в линейном случае не будет особого вреда считать их числами. Они не меняются при изменении независимой переменной. Моя дочь получала бы 10 долларов в час, сколько бы часов ни работала, а уклон пандуса для колясок составляет 1/12 в любой его точке. Однако не дайте себя одурачить. Эти коэффициенты – все равно функции. Просто это постоянные функции. График постоянной функции – это горизонтальная линия, как показано на следующем рисунке для хлеба с изюмом и корицей, который всегда дает 200 калорий на ломтик.

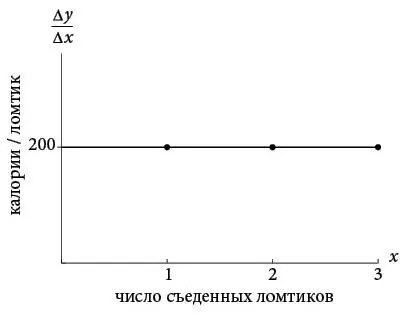
Когда в следующем разделе мы перейдем к нелинейным зависимостям, то увидим, что они на координатной плоскости дают не прямую, а кривую. В любом случае прямая или кривая всегда многое говорят о той взаимосвязи, которая их породила. Это словно фотография крупным планом или подпись. Это ключ к пониманию того, что их создало.

Обратите внимание на разницу между функцией и графиком функции. Функция – это бестелесное правило, которое берет на входе разные x и выдает на выходе по одному y для каждого x . В этом смысле функция бесплотна. Когда вы смотрите на нее, вам не на что смотреть. Это призрачная сущность, абстрактное правило. Например, оно может быть таким: «Дайте мне число, и я верну число, в 10 раз большее». Напротив, график функции – это видимая, почти осязаемая штука, некая форма, которую вы можете видеть. В частности, график только что описанной мною функции будет прямой, проходящей через начало координат, с угловым коэффициентом 10, то есть определяемой уравнением y = 10 t . Однако сама функция – это не прямая. Функция – это правило , которое порождает эту прямую. Чтобы выявить саму функцию, вам нужно накормить ее x , дать выплюнуть y , повторить это для всех x и зафиксировать результаты. Когда вы это делаете, сама функция остается невидимой. То, что вы видите, – это ее график.

Нелинейная функция и ее скорость изменения

Когда функция не линейна, ее скорость изменения Δ y / Δ x не будет постоянной величиной. В геометрических терминах это означает, что график функции представляет собой кривую с наклоном, который меняется от точки к точке. В качестве примера рассмотрим параболу на следующем рисунке:

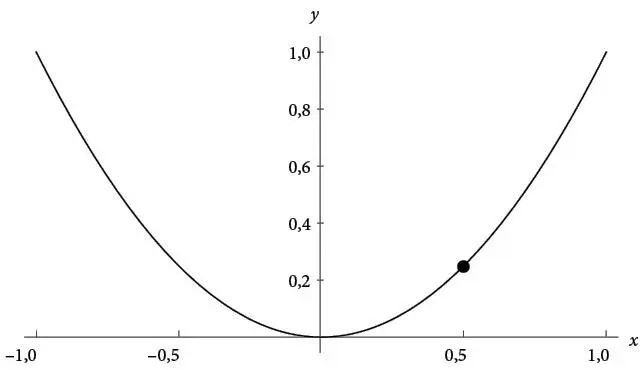
Это кривая y = x 2, которая соответствует простейшей нелинейной функции на калькуляторе, квадратичной функции x 2. Такой пример даст нам некоторую практику с определением производной как наклона (углового коэффициента) касательной, а также разъяснит ограничения подобного определения.

Рассматривая параболу, мы видим, что одни ее части крутые, а другие относительно пологие. В точке x = 0 парабола горизонтальна, и мы без труда понимаем, что производная в этой точке должна равняться 0, потому что касательная линия в этой точке, очевидно, совпадает с осью x . Линия не поднимается и не опускается, а значит, ее наклон должен быть равен 0.

Однако на первый взгляд неясно, каков наклон параболы в других точках. Фактически он вообще неочевиден. Чтобы разобраться в этом, давайте проведем мысленный эксперимент в духе Эйнштейна и представим, что бы мы увидели, если бы начали смотреть на произвольную точку ( x, y ) с большим увеличением, словно увеличиваем масштаб при фотографировании, оставляя эту точку в центре кадра. Это похоже на то, как будто мы смотрим на нее в микроскоп и постепенно добиваемся все большего увеличения. По мере увеличения прилегающий к точке кусок параболы будет все сильнее напоминать прямую. В пределе при бесконечно большом увеличении (это означает, что мы смотрим на бесконечно маленький кусочек кривой вокруг интересующей нас точки) данный увеличенный кусочек должен приблизиться к прямой. Тогда эта предельная прямая линия определяется как касательная в данной точке кривой, а угловой коэффициент как производная в этой точке.