М. Фартушняк - Репетитор по математике. Алгебра

Теперь, как оценивать тестовые задания. За каждое правильное тестовое задание начисляется 1 балл. По количеству набранных баллов и выставляется итоговая оценка по 12-ти бальной системе. Например, вы ответили правильно на 7 вопросов-это оценка 4-. При 11-ти верных ответах имеете оценку 5, а при 12-ти имеете максимум 5+.

Продолжительность тестирования – 25—30 минут. Выделите для тестирования отдельный день. Берите чистый лист бумаги и вперёд. Тесты – это не только интересно, но и познавательно. Желательно пройти все предложенные тесты (но не более двух за один день), в конце книги имеются ответы на тестовые задания для проверки. Не стоит в них заглядывать раньше времени.

Задачи для самостоятельного решения.Автор сознательно не выделял какими-то знаками задания повышенной сложности и считает, что такое приём способствует более спокойному решению задач без излишнего волнения и стресса. В процессе решения вы сами сможете понять, сложна для вас данная задача или нет. Притом сложность задачи – это субъективная оценка. Некоторые с лёгкостью могут решать подобные задачи, а вот более простые в нашем понимании могут вызвать затруднение. Если вы поняли, что можете приступать к решению задач, то не медлите. Каких-то ограничений по количеству решаемых задач в день нет. Когда поняли, что устали, то занятие можно прекратить, но хотя бы 30 – 40 минут в день вы должны уделять решению задач. Это не обязательно делать изо дня в день. Через какое-то время можно сделать себе 1- 2-х дневный перерыв. Но с отдыхом не затягивайте. Почувствовав, что немного отдохнули и есть свободное время, приступайте снова к решению задач. Автор рекомендует решить все задачи, которые есть в разделе для самостоятельного решения. Решив какую-то задачу, загляните в раздел «ответы» и, убедившись, что вы все решили правильно, продолжайте дальше. Если ваш ответ не совпадает с ответом в конце книги, рекомендуется ещё раз пройтись по своему решению и выявить ошибки. Если вы их не обнаружили, то загляните в раздел «Указания к решению задач». Он находится после раздела ответов. Прочитав указания к решению задач (они есть практически ко всем задачам), снова приступайте к решению сложной для вас задачи. К задачам для самостоятельного решения есть полные и подробные решения, которые находятся в соответствующем разделе. Но это последний раздел, в который вам следует заглянуть. Это в том случае, когда задача не решается без посторонней помощи. Не злоупотребляйте этим разделом, иначе вы так никогда и не научитесь решать математические задачи. Постарайтесь ограничиться только разделом «Указания к решению задач». Этого бывает достаточно, чтобы понять свою проблему и попытаться её искоренить.

В конце книги, как я уже сказал, находится справочный раздел, ответы к тестовым заданиям, ответы к задачам для самостоятельного решения, указания к решению задач, решение задач. Кроме этого, там же находится список использованной литературы. Структура книги максимально удобна для использования. А в начале книги предложены условные математические обозначения, которые будут встречаться в дальнейшем.

Автор будет благодарен за любые замечания и обнаруженные неточности и ошибки при написании этого пособия. А также будет рад любому мнению и практическим советам от учителей и преподавателей математики по улучшению данной книги.

Это один из основных разделов математики. В нем мы научимся преобразовывать алгебраические выражения, решать разнообразные уравнения, неравенства, а также их системы (в том числе показательные и логарифмические). Большое внимание уделим текстовым задачам, а также ознакомимся с понятием «функция» и научимся строить графики различных функций. Просьба, по возможности, решить все предложенные задачи в этом разделе и пройти все тестовые задания.

Возвести число в целую степень n, значит повторить его сомножителем n раз т.е.

Вторая степень называется квадратом, третья – кубом.

Запомните!

1) Первой степенью числа называют само это число.

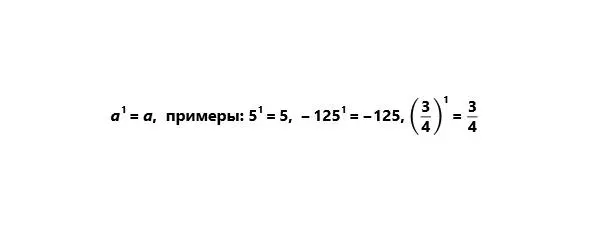
2) Любое число (кроме нуля) в нулевой степени есть единица.

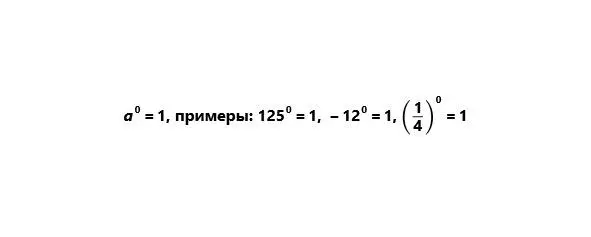
3) Нуль в любой неотрицательной степени есть нуль.

4) Единица в любой степени есть единица.

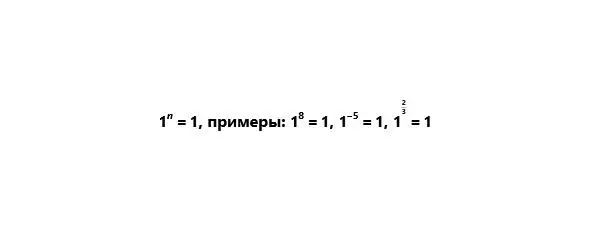
Отрицательный показатель степени.

Дробный показатель степени.

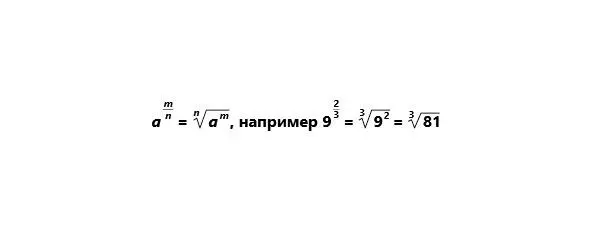
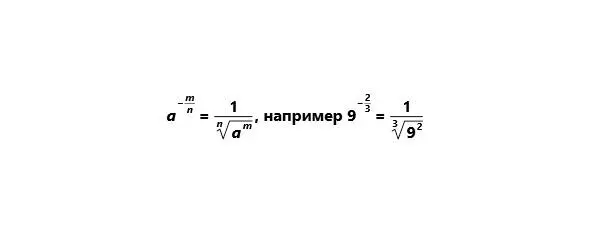
Дробный отрицательный показатель степени

Теперь рассмотрим свойства степени. Для удобства мы составили таблицу, в котором привели примеры не только с натуральными показателями степени, но и с рациональными и действительными.

Необходимые пояснения к свойствам степени.

Первые два свойства указывают на действия со степенями с одинаковыми основаниями. При умножении таких степеней их показатели складываются (свойство 1), при делении – вычитаются (свойство 2). Третье свойство – это свойство возведения степени в степень – показатели степени перемножаются (свойство 3).

Следующие два свойства – это возведение в степень произведения (свойство 4) и частного (свойство 5). Притом, свойство 4 справедливо для любого числа сомножителей. Применение данных правил позволяет существенно облегчить вычисления.