М. Фартушняк - Репетитор по математике. Алгебра

Извлечение корня есть нахождение основания степени по степени и её показателю. Записывается это так

Основные свойства корня.

1) Если за корнем следует степень, равная показателю корня,

то корень можно опустить, например

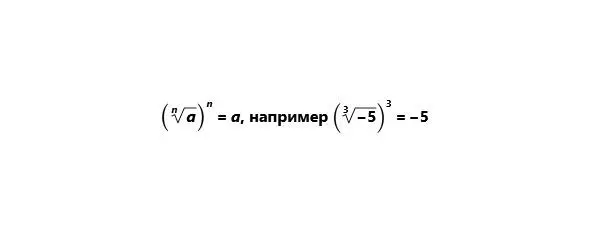
2) Если подкоренное число имеет степень равную

показателю корня, то оно равно модулю подкоренного числа.

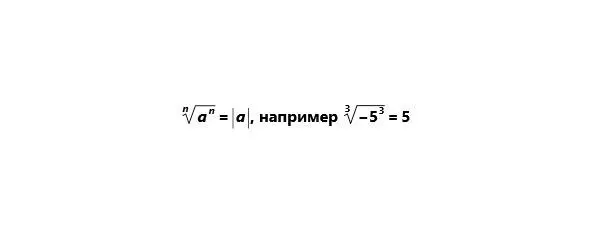
Основные действия с корнями (все эти правила справедливы при

a≥0 и b≥0)

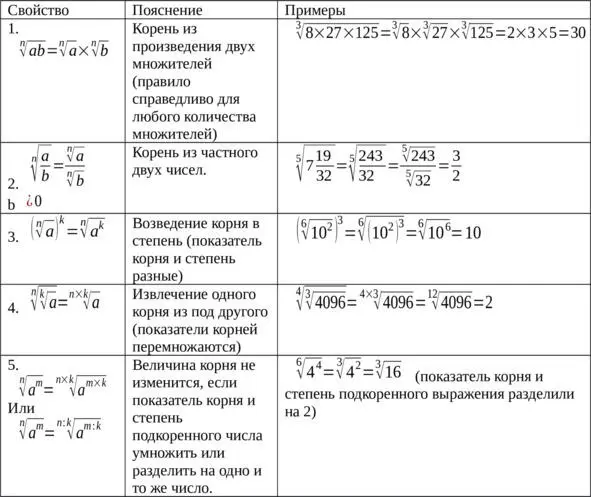
Все вышеизложенные правила позволяют существенно облегчить вычисления.

Рассмотрим две операции: внесение множителя под знак корня и вынесение множителя из-под знака корня при решении задач.

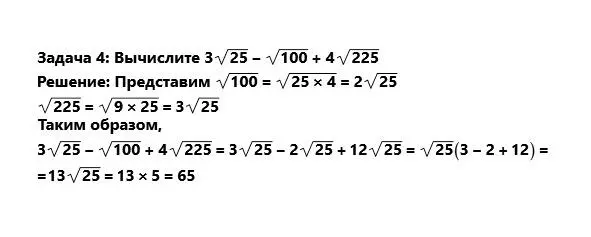
Очень часто при преобразованиях пользуются приёмом уничтожения иррациональности в знаменателе или числителе дроби. Такой метод позволяет упростить приближенные вычисления. Рассмотрим его на примере.

.

Уничтожив иррациональность в знаменателе, мы пришли к такому результату, что нам необходимо разделить приближенное число на целое, что намного точнее и проще, чем делить приближенное число на приближенное и проводить вычисления с большим количеством значащих цифр, чтобы получить два верных знака после запятой.

Мы подошли к одной из самых важных тем алгебры. Ведь без задания на преобразование алгебраических выражений не обходится практически ни один экзамен по математике. Сразу предупреждаю, такие преобразования сложны и требуют не только знаний, но и внимания, смекалки, терпения.

Для начала мы ознакомимся с понятиями «одночлен» и «многочлен».

Одночленом называется произведение двух или нескольких сомножителей каждый из которых есть либо число, либо буква, либо степень буквы.

Например, 6a 2x, 2c, 3b 3c 2, -10y 7, -7abc.

Одночлены состоят из коэффициента (числового множителя) и буквенной части.

6a 2x = 6 (коэффициент) × a 2x (буквенная часть).

Отдельно взятое число, буква или степень буквы тоже рассматриваются как одночлен. Например, -5 (одночлен без буквенной части), с и c 5(одночлены, в которых коэффициент равен 1).

Одночлены называются подобными, если они одинаковы или отличаются только коэффициентами.

Например, 7x 2y 3, -5x 2y 3, -x 2y 3 – подобны.

Сложение двух или нескольких одночленоввозможно только тогда, когда среди слагаемых имеются подобные.

Например, 6x 2y 2+9x 2y 2 – 7x 2y 2= 8x 2y 2.

Здесь мы суммировали коэффициенты, оставив буквенную часть без изменений. Такое действие называется приведением подобных членов.

Можно этот пример решить иначе, вынеся общий множитель за скобки:

6x 2y 2+9x 2y 2 – 7x 2y 2= (6+9—7) x 2y 2= 8x 2y 2.

Как мы видим, вынесение общего множителя за скобки – операция, идентичная приведению подобных членов.

Произведение двух или нескольких одночленовможно упростить лишь тогда, когда в них входят некоторые степени одних и тех же букв или числовые коэффициенты. При этом показатели степеней у соответствующих букв складываются, числовые коэффициенты перемножаются.

Пример: -10x 2y×3x 3y 2× (-xy 3) = -10×3× (-1) (x 2x 3x) (yy 2y 3) = 30x 6y 6.

Для лучшего понимания, мы расписали это действие более подробно, хотя оно довольно прозрачное и может делаться устно.

Частное двух одночленовможно упростить, если делимое и делитель содержат некоторые степени одних и тех же букв или числовые коэффициенты. При этом показатель степени делителя вычитается из показателя степени делимого, а числовой коэффициент делимого делится на числовой коэффициент делителя.

Пример: 6x 3y 8z 7: 2xy 5z 3= 3x 2y 3z 4.

Здесь числовой коэффициент делимого разделили на числовой коэффициент делителя, вычли показатели степени буквы x (3—1=2), буквы y (8—5=3) и буквы z (7—3=4).

При делении двух одночленов могут возникнуть две ситуации, которые требуют дополнительного пояснения.

1.Если показатели степени у некоторой буквы в делимом и делителе одни и те же, то в частное эта буква не войдёт (ведь нулевая степень любого числа равна единице).

Пример: 12x 3y 4: 4x 3y 2=3y 2.

2.Если показатель степени какой-нибудь буквы в делимом меньше, чем показатель степени той же буквы в делителе, то вычитание даёт отрицательную степень этой буквы.

Пример: 8x 3y 5: 2x 5y 3= 4x -2y 2= (4y 2) / (x 2)

При возведении одночлена в степеньиспользуется правило возведения степени в степень.

Пример: Возведём одночлен 2a 4b 2в четвертую степень.

(2a 4b 2) 4 = 2 4 (a 4) 4 (b 2) 4 = 16a 16b 8.

Не забывайте, что показатели степеней при данном правиле перемножаются.

Сумма одночленов называется многочленом.