М. Фартушняк - Репетитор по математике. Алгебра

Например, 4x 2y +3a -7b 2 – многочлен, состоящий из суммы одночленов 4x 2, 3a, -7b 2.

При сложении и вычитании многочленов снова получается многочлен.

Пример. Сложим многочлены x 3+2x 2y 2 – 7x 2+ y и 3x 3 – x 2y 2+5x 2 – 3y.

Составим сумму многочленов, затем раскроем скобки и приведём в полученном многочлене подобные члены.

(x 3+2x 2y 2—7x 2+y) + (3x 2– x 2y 2+5x 2 – 3y) = x 3+3x 3+2x 2y 2 – x 2y 2 – 7x 2 +5x 2+ y – 3y = 4x 3+ x 2y 2 – 2x 2 – 2y.

Здесь одновременно с раскрытием скобок мы сгруппировали подобные члены (для удобства вычислений).

Аналогично, производится и вычитание многочленов. Не забывайте, если перед скобкой стоит знак «минус», то все члены, заключаемые в скобки, меняют свой знак на противоположный.

Пример. (4x 2y – 7x 3+5y – 3) – (-2x 2y +5x 3– 3y +2) =4x 2y – 7x 3+5y -3 +2x 2y -5x 3+3y – 2 = 6x 2y – 12x 3+8y – 5.

Произведение многочленов.

Произведение одночлена и многочлена всегда можно представить в виде многочлена.

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Схема: a× (b+c) =a×b+a×c (открытие скобок)

Например:

– 4x 3(2y 3– x +6) = -4x 32y 3+ (-4x 3(-x)) + (-4x 3×6) = -8x 3y 3+4x 4 – 24x 3.

Мы выписали здесь промежуточные вычисления, хотя, в принципе, без этой записи можно обойтись.

Умножение многочлена на многочлен.

Произведение многочлена на многочлен равно сумме всех возможных произведений каждого одночлена одного из многочленов на каждый одночлен другого.

Схема: (a+b) × (c+d) =a×c+a×d+b×c+b×d

Пример. (3x 2 – 6x +2) × (4x 3 – 3x) = 12x 5 – 9x 3 – 24x 4+18x 2+8x 3 – 6x =

= 12x 5 – 24x 4 – x 3+18x 2 – 6x.

Существуют частные случаи умножения многочленов, которые называются формулами сокращённого умножения многочленов. Их желательно запомнить.

1. (a+b) 2 =a 2+2ab+b 2(квадрат суммы)

2. (a-b) 2=a 2—2ab+b 2(квадрат разности)

3. (a-b) (a+b) =a 2-b 2(разность квадратов)

4. (a+b) 3=a 3+3a 2b+3ab 2+b 3(куб суммы)

5. (a-b) 3=a 3—3a 2b+3ab 2-b 3(куб разности)

6. (a+b) (a 2-ab+b 2) =a 3+b 3(сумма кубов)

7. (a-b) (a 2+ab+b 2) =a 3-b 3(разность кубов)

Примеры: (2ma 2+0.1nb 2) 2 = 4m 2a 4+0.4mna 2b 2+0.01n 2b 4

(5x 3 – 2y 3) 2 = 25x 6 – 20x 3y 3 +4y 6

(0.2a 2b + c 3) (0.2a 2b – c 3) = 0.04a 4b 2 – c 6

(5ab 2+2a 3) 3 = 125a 3b 6+150a 5b 4+60a 7b 2 +8a 9

Предлагаю вам самим узнать, какие формулы были использованы в этих примерах.

Деление многочленов.

1. Деление многочлена на одночлен.

Частное от деления многочлена на одночлен равно сумме частных, полученных от деления каждого слагаемого многочлена на одночлен.

Схема:

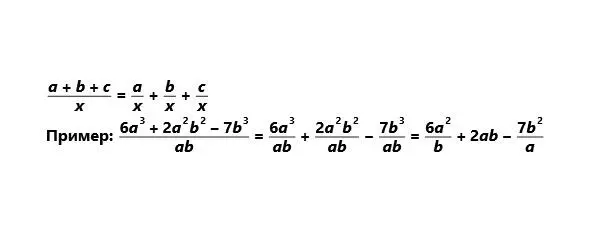
2. Деление многочлена на многочлен в общем случае можно выполнить с остатком, подобно тому, как это делается при делении целых чисел.

Разделить многочлен P на многочлен Q значит найти многочлен M (частное) и N (остаток) удовлетворяющий двум требованиям: 1) должно соблюдаться равенство MQ+N=P и 2) степень многочлена N должна быть ниже степени многочлена Q.

Процесс нахождения частного M и остатка N аналогичен процессу деления с остатком многозначного числа на многозначное. Перед делением члены делимого и делителя располагается в порядке убывания степеней главной буквы.

Например, разделим 6x 3+2x 2 – x +12 на 3x 2 – 2x +6

Запись деления:

1.Делим первый член делимого 6x 3на первый член делителя 3x 2. Результат 2x – первый член частного.

2.Умножаем полученный член на делитель 3x 2 – 2x +6, результат 6x 3 – 4x 2+12x записываем под делимым.

3.Вычитаем члены результата из соответствующих членов делимого, сносим следующий по порядку член делимого, получаем 6x 2 – 13x +12

4. Первый член остатка 6x 2делим на первый член делимого, результат 2 есть второй член частного.

5. Множим полученный второй член частного на делитель, результат 6x 2 – 4x +12 подписываем под первым остатком.

6. Вычитаем члены этого результата из соответствующих членов первого остатка, получаем второй остаток: -9x. Его степень меньше степени делителя. Деление закончено.

.

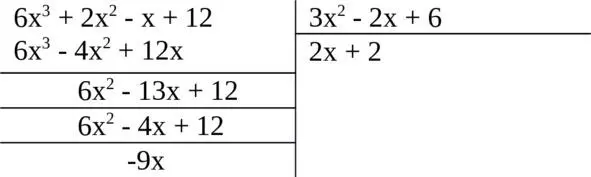
Целая часть: 2x +2

Остаток: – 9x

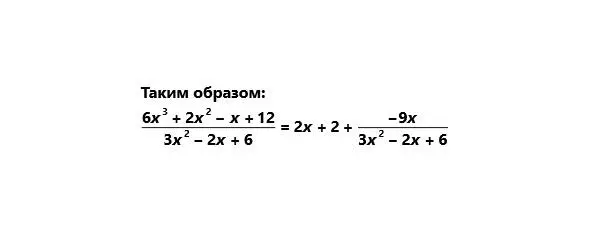
Приведём более сложный пример без дополнительных пояснений.

Целая часть: 3t 2 – 7t +5

Остаток: 34t – 37

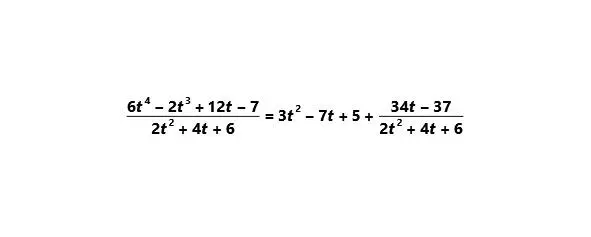
Среди частных случаев деления многочлена на многочлен выделим делимость двучлена x m±a mна x±a.

1. Разность одинаковых степеней двух чисел делится без остатка на разность этих чисел, т.е. x m-a mделится на x-a

Примеры.

(x 2-a 2): (x-a) =x+a

(x 3-a 3): (x-a) =x 2+ax+a 2

(x 4-a 4): (x-a) =x 3-ax 2+a 2x+a 3

(x 5-a 5): (x-a) =x 4-ax 3+a 2x 2+a 3x+a 4

2. Разность одинаковых чётных степеней двух чисел делится не только на разность этих чисел, но и на их сумму т.е. x m-a mпри чётном m делится на x+a

Примеры.

(x 2-a 2): (x+a) =x-a

(x 4-a 4): (x+a) =x 3-ax 2+a 2x-a 3

(x 6-a 6): (x+a) =x 5-ax 4+a 2x 3-a 3x 2+a 4x-a 5

2a. Разность одинаковых нечётных степеней двух чисел не делится на сумму этих чисел.

Например, ни x 3-a 3, ни x 5-a 5не делятся на x+a.

2б. Так как разность чётных степеней делится на x-a и на x+a, то она делится и на x 2-a 2.

Примеры.

(x 4-a 4): (x 2-a 2) =x 2+a 2

(x 6-a 6): (x 2-a 2) =x 4+a 2x 2+a 4

(x 8-a 8): (x 2-a 2) =x 6+a 2x 4+a 4x 2+a 6

3. Сумма одинаковых степеней двух чисел никогда не делится на разность этих чисел.

Например, ни x 2+a 2, ни x 3+a 3не делятся на x-a.

4. Сумма одинаковых нечётных степеней двух чисел делится на сумму этих чисел.

Примеры.

(x 3+a 3): (x+a) =x 2-ax+a 2

(x 5+a 5): (x+a) =x 4-ax 3+a 2x 2-a 3x+a 4

4а. Сумма одинаковых чётных степеней двух чисел не делятся ни на разность, ни на сумму этих чисел.

Например, x 6+a 6не делится ни на x-a, ни на x+a.

Запомнить эти формулы необязательно, но уметь их применять необходимо.

Для удобства и упорядочивания вышеизложенных сведений можно составить такую таблицу.

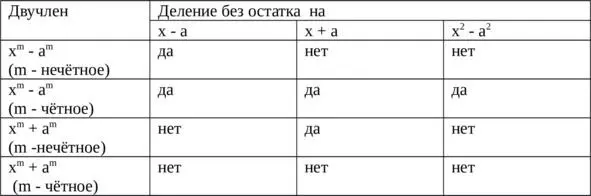
Возведение в степень n двучлена a+b.

(a+b) n=a n+k 1×a n-1×b+k 2×a n-2×b 2+…+b n(эта формула называется биномом Ньютона).

Где коэффициенты k (биноминальные коэффициенты) определяются из треугольника Паскаля.

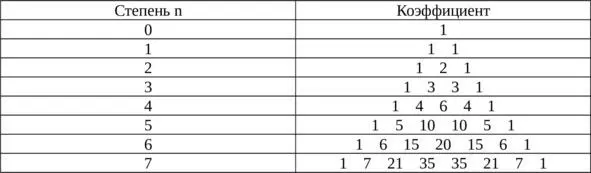
Треугольник Паскаля – таблица бесконечная. Вершина таблицы и боковые стороны каждой строки имеют единицы. Остальные числа (в середине) равны сумме 2-ух чисел, которые находятся в предыдущей строке (над ними).Вы можете легко это проверить, а также потренироваться в составлении коэффициентов для степени 8. Теперь, зная секрет этой таблицы, вы можете без труда вычислить необходимые коэффициенты. Запомните только, что таблица начинается с нулевой степени.