Яков Перельман - Живой учебник геометрии

Итак, мы убедились, что

к а т е т п р о т и в у г л а в 30° р а в е н п о л о в и н е г и п о т е н у з ы.

Применения

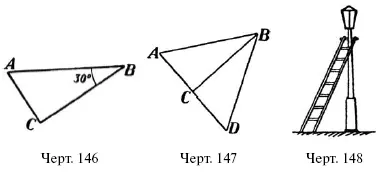
58. Лестница длиною 6 м приставлена к фонарному столбу под углом 30° к нему (черт 148). Каково расстояние от основания лестницы до основания фонаря?

Р е ш е н и е. Так как катет против 30° равен половине гипотенузы, то искомое расстояние = 3 м.

59. Длина стропильной ноги АС (черт. 137) вдвое больше высоты AD стропильной фермы. Определить угол наклона этой кровли к горизонту.

Р е ш е н и е. Искомый угол СAD = 30°, так как только при таком условии CD равно половине АС .

Пусть у нас имеется прямоугольный треугольник (черт. 146) ABC , один угол которого, именно В , равен 30°. Перегнем мысленно треугольник по катету ВС . Тогда займет положение ВСD (черт. 147), при чем CD составит продолжение АС , потому что уг. ВСD + ВСА = развернутому. Уг. СВD = уг. ABC = 30°; значит, уг. А = 60°;

Мы знаем, что если в треугольнике есть равные стороны, то углы, лежащие против них, тоже равны. Рассмотрим теперь, каково соотношение между сторонами и углами в случае н е р а в н ы х сторон.

Предварительное упражнение

В фигуре черт. 149 укажите какой угол больше: уг. 1 или у г. 2?

В фигуре черт. 151 АВ = AD . Какой угол больше; уг. С или у г. 1?

Покажем, что в

т р е у г о л ь н и к е с н е р а в н ы м и с т о р о н а м и п р о т и в б о л ь ш е й с т о р о н ы л е ж и т б о л ь ш и й у г о л. Пусть в треугольнике АВС (черт. 150) сторона АС больше «стороны АВ . Отложим от вершины образуемого ими угла меньшую сторону АВ на большей АС получим точку D . Соединив D с В , имеем равнобедренный треугольник ABD , в котором угол 1 = уг. 2. Угол С меньше угла 1, а значить, подавно меньше угла. ABC . Таким образом мы убеждаемся, что против большей стороны [АС] лежит больший угол [ABC] .

Нетрудно удостовериться, что и обратно: если в треугольнике имеются неравные углы, то

п р о т и в б о л ь ш е г о у г л а л е ж и т б о л ь ш а я с т о р о н а.

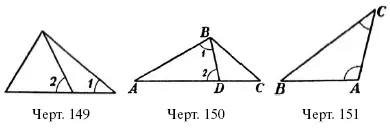
Пусть мы знаем, что в треугольнике (черт. 151) ABC уг. А больше угла С . Тогда сторона ВС не может быть равна АВ : иначе уг. А равнялся бы углу С ; не может сторона ВС быть и м е н ь ш е: АВ – тогда уг. А был бы м е н ь ш е угла С (а мы знаем, что уг. А б о л ь ш е уг. С ). Не равен и не меньше, значит – больше.

Применения

60. Что больше: гипотенуза или катет?

Р е ш е н и е. Гипотенуза, как сторона, лежащая против самого большого угла треугольника, длиннее каждого катета.

61. Угол при вершине равнобедренного треугольника = 70°. Что длиннее: основание или боковая сторона?

Р е ш е н и е. Углы при основании равны (180°-70°) / 2 = 65°.

Так как угол прш вершине больше, то основание больше боковых сторон.

Повторительные вопросы к §§ 48–53

Каково соотношение между углами треугольника, две стороны которого равны? – каково соотношение между сторонами треугольника, имеющего два равных угла? – Каковы соотношения в треугольнике с неравными сторонами? – С нерав-нымиуглами? – Какой треугольник называется равнобедренным? – Какая сторона такого треугольника называется боковой? – Какая называется основанием? – Как называется треугольник, имеющий два равных угла? – Сколько градусов в угле, опирающемся на диаметр? – Какой треугольник называется прямоугольным? – Что называется гипотенузой? – Катетами? – По каким признакам можно установить равенство прямоугольных треугольников? – Какой треугольник называется равносторонним? – Как велики его углы? – Каково соотношение между гипотенузой и катетом, лежащим против угла в 1/3 прямого?

Если из точки проведен к прямой перпендикуляр, – например, CD (черт. 152), то точка D называется

о с н о в а н и е м п е р п е н д и к у л я р а. Всякая другая линия, проведенная через точку С к прямой А В, встречает ее не под прямым углом (почему?) и называется наклонной; например, СЕ, CF – наклонные. Точки Е, F – о с н о в а н и я наклонных.

Расстояния DE, DF от основания перпендикуляра до оснований наклонных называются проекциями этих наклонных: DE – проекция наклонной СЕ , a DF – проекция наклонной CF .

Рассмотрим некоторые соотношения между перпендикуляром, наклонными и их проекциями.

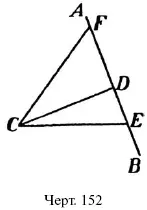
1) Перпендикуляр короче каждой наклонной, проведенной к той же прямой из той же точки. Например, CD на черт. 152 короче, чем CF и чем СЕ , потому что катет короче гипотенузы. Перпендикуляр есть поэтому самое короткое расстояние от точки до прямой. Когда говорят о расстоянии точки от какой-нибудь прямой, то имеют в виду именно к р а т ч а й ш е е расстояние,

т. е. п е р п е н д и к у л я р из точки на эту прямую.

2) Если из какой-нибудь точки проведены к прямой две наклонные о д и н а к о в о й длины, – напр., АВ и АС на черт. 153, то проекции этих наклонных р а в н ы. В самом деле: треугольники ABD и ACD имеют общий катет AD , равные гипотенузы АВ и АС и кроме того, уг. B = уг. С (§ 52); поэтому они равны ( СУС ), и значит, катет ОВ = катету DC .

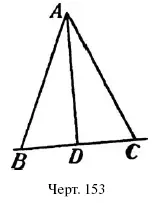
3) Обратно: если равны проекции двух наклонных, проведенных к прямой из одной точки, то эти наклонные имеют одинаковую длину. Если бы на черт. 153 нам не было известно, что наклонные АВ и АС равны, но взамен этого мы знали бы, что BD = DC , то установили бы равенство АВ и АС из равенства прямоугольных треугольников ADB и ADC ( СУС ).

Сейчас мы установили, что при равных проекциях наклонные равны. Отсюда вытекает важное свойство перпендикуляра, проведенного через середину стороны. А именно: если через середину С отрезка АВ (черт. 154) проведена перпендикулярно к нему прямая EF , то каждая точка этого перпендикуляра удалена от концов отрезка одинаково. Например, точка М одинаково отстоит от точек А и В . Это следует из того, что проекции ВС и АС наклонных MB и МА равны, – значит, равны и наклонные. Точно также равны расстояния NА и NB. Вообще