Яков Перельман - Живой учебник геометрии

Треугольник с двумя равными сторонами называетс я р а в н о б е д р е н н ы м; его равнее стороны называются б о к о в ы м и с т о р о н а м и этого треугольника, а третья сторона – его о с н о в а н и е м.

Поэтому рассмотренное сейчас свойство треугольника можно высказать короче так:

в р а в н о б е д р е н н о м т р е у г о л ь н и к е у гл ы п р и о с н о в а н и и р а в н ы.

Можно удостовериться и в обратном соотношении: если в треугольнике имеются равные углы, то стороны, лежащие против этих углов, – равны; или-короче сказать:

в т р е у г о л ь н и к е п р о т и в р а в н ы х у г л о в л е ж а т р а в н ы е с т о р о н ы.

Чтобы убедиться в этом, возьмем треугольник (черт. 135), в котором два угла равны: уг. B = уг. C . Проведем (черт. 136) равноделящую AD ; в образовавшихся двух треугольниках ADB и ADC сторона AD – общая, уг. BAD = уг. CAD, уг. В = уг. C ; следовательно, треугольники равны ( УСУ ), и потому АВ = АС .

Применения

52. Огород имеет форму равнобедренного треугольника, одна сторона которого на 40 м длиннее другой. Обвод огорода 200 м. Какова длина каждой стороны? Сколько решений имеет эта задача?

Р е ш е н и е. Если оcнование этого треуголь ника больше боковых сторон, то, обозначив его через х , имеем уравнение

х + х – 40 + х – 40 = 200,

из которого находим: х =280/3 = 93 1/3 м.

Значит, в таком случае стороны треугольника имеют длину: 93 1/3 м, 531/3 м и 531/3 м.

Если же основание к о р о ч е боковых сторон, то составляем уравнение

y + y + 40 + y + 40 = 200,

из которого y = 40 м. Следовательно, второе решение задачи 40 м, 80 м и 80 м.

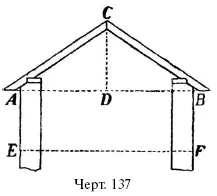
53. Кровля, в зависимости от материала, из которого она сделана, должна составлять с горизонтальной линией следующие углы (черт. 137):

Железная и цинковая. . . 30°

Толевая. . . . . . . . . . 18°

Черепичная. . . . . . . . 40°

Тесовая. . . . . . . . . . 45°

Соломенная. . . . . . . . 60°

Зная это, определите, какой угол должны составлять между собой стропильные ноги двускатной крыши в каждом случае.

Р е ш е н и е. Для железной кровли искомый угол равен 180° – 2 ? 300 = 120°; для толевой 180° – 2 ? 18° = 144°; для черепичной 180° – 2 ? 40° = 100°; для тесовой 180° – 2 ? 45° = 90°; для соломенной 180° – 2 ? 60° = 60°.

Из свойств равнобедренного треугольника вытекает следующая особенность угла, вписанного в полукруг (черт. 138) или: как его иначе называют – «опирающего на диаметр»:

У г о л, о п и р а ю щ и й с я н а д и а м е т р, р а в е н п р я м о м у.

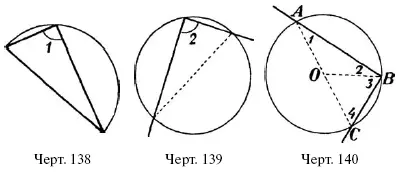
«Опирающимся на диаметр», или «вписанным в полукруг» называют такой угол, вершина которого лежит на дуге окружности, а стороны проходят через концы диаметра; таковы углы: 1 на черт. 138 и 2 на черт. 139. Желая удостовериться, что такой угол во всех случаях равен 90°, мы соединяем центр О полукруга (черт. 140) с вершиной В угла. Получаем два равнобедренных треугольника АОВ и ВОС (почему они равнобедренные?). В них

уг. 2 = уг. 1

уг. 3 = уг. 4.

Отсюда уг. 2 + уг. 3 (т. е. уг. АВС ) = уг. 1 + уг. 4. Но так как уг. АВС + уг. 1 + уг. 4 = 180°, то уг. ABC = 90°.

Этим свойством окружности пользуются нередко для того, чтобы в изделиях проверять полуокружность помощью чертежного треугольника (как?).

В треугольнике, мы знаем, может быть только один прямой угол. Такой треугольник называется п р я м о у г о л ь н ы м. Стороны прямоугольного треугольника имеют особые названия: каждая из сторон, между которыми лежит прямой угол, называется к а т е т о м, а сторона против прямого угла называется г и п о т е-н у з о й.

Применения

54. Через точку С (черт. 141) на прямой MN нужно провести перпендикуляр. Как это сделать?

Р е ш е н и е. Отложив (черт. 142) от С в обе стороны по какому-нибудь равному отрезку, т. е. CA = CB , описываем около А и В , как центров, каким-нибудь радиусом дуги; прямая PC , соединяющая точку Р пересечения дуг с точкой С , перпендикулярна к МN . Действительно, треугольники АР С и ВРС , получающиеся после соединения А и В с P , равны ( СУС ); следовательно, уг. АСР = уг. ВСР , а так как эти углы смежные, то они – прямые.

55. Через точку С (черт. 143) вне прямой МN про вести к этой прямой перпендикуляр.

Р е ш е н и е. Около точки С, как около центра, описываем каким-нибудь радиусом дугу АВ (черт. 144);

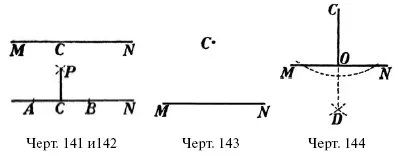
затем около точек А и В каким-нибудь радиусом описываем дуги D . Прямая DС перпендикулярна к МN . Чтобы убедиться в этом, соединим С и D с А и В .

Треугольники ACD и ВCD равны ( ССС ), следовательно, уг. ACD = уг. DCВ , и значит, треугольник АСО = ВСО ( СУС ). Отсюда уг. AОС = уг. ВОС , а так как эти углы смежные, то они прямые.

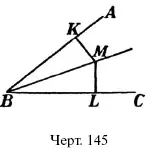
56. Объясните, почему каждая точка М прямой ВM , делящей пополам угол АВС (черт. 145) одинаково отстоит от сторон АВ и ВС угла (т. е. почему, например, MK = ML ?).

Р е ш е н и е. Треугольники ВML и ВМК равны ( УСУ ).

Треугольник с тремя равными сторонами называется р а в н о с т о р о н н и м. Так как против равных сторон в одном и том же треугольнике лежат равные углы, то все углы равностороннего треугольника равны, и, следовательно, каждый из них равен. 180°: 3 = 60°.

Обратно: если каждый угол треугольника равен 60°, то все стороны такого треугольника одинаковы, – потому что, против равных углов в одном и том же треугольнике лежат, равные стороны.

Применения

57. Без транспортира построить угол в 60°. В 30°. В 15°. В 120°. В 75°.

Р е ш е н и е. Строим равносторонний треугольник произвольных размеров; каждый его угол = 60°. Разделив угол этого треугольника пополам, получим угол в 30°. Разделив еще раз пополам, будем иметь угол в 15°. Угол в 120° = 90° + 30°. Угол в 75° =60° + 15° = 90° – 15°.

Предварительное упражнение

Равносторонний треугольник разбит равноделящей одного из углов на два треугольника. Определить их углы.

уг. D = 60°; а так как и уг. ABD = 60°, то треугольник ABD – равносторонний, и следовательно, AD = АВ . Но АС = 1/2 АD (почему?); отсюда АС = 1/2 АВ .