Яков Перельман - Живой учебник геометрии

Р е ш е н и е. Мы имеем в этом случае ряд параллельных прямых, проведенных через равноудаленные друг от друга точки одной стороны угла; они должны отсечь от другой стороны угла (т. е. от края доски) равные отрезки.

65. Середины сторон прямоугольника с диагональю 10 см последовательно соединены прямыми линиями. Найти обвод образовавшегося четырехугольника.

Р е ш е н и е. Каждая сторона этого четырехугольника равна половине диагонали (как линия, соединяющая середину двух сторон треугольника), т. е. 5 см. Значит обвод четырехугольника = 20 см.

Предварительные упражнения

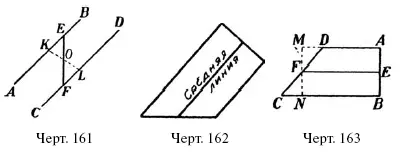
На черт. 161 прямые АВ и CD параллельны. Прямая KL проведена через середину О отрезка EF . Докажите, что треугольники КОЕ и FOL равны.

В четырехугольнике AFED (черт. 155) сторона AF - DE и параллельна ей. Докажите, что этот четырехугольник есть параллелограмм.

С р е д н е й л и н и е й трапеции называется прямая, соединяющая середины ее непараллельных сторон (черт. 162). Этот отрезок обладает следующим свойством:

с р е д н я я л и н и я т р а п е ц и и р а в н а п о л у с у м м е е е о с н о в а н и й.

Удостовериться в этом можно так. Пусть в трапеции ABCD (черт. 163) прямая EF есть средняя линия, т. е. соединяет середины непараллельных сторон АВ и DC . Проведем через точку F прямую, параллельную АВ и продолжим AD до пересечения с сейчас проведенной линией. Треугольники FDM и FNC равны ( УСУ ), следовательно, MD = NC. Четырехугольник EBNF есть параллелограмм ( EB = l/2 AB; FN = 1/2 MN; AB-=MN ; значит, ЕВ равно и параллельно FN и т. д.); поэтому EF = BN . Точно так же EF = AM . Зная это, пишем:

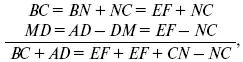
а откуда:

EF = BC + AD/2

Мы убедились, что во всякой трапеции средняя линия равна полусумме ее оснований. Вспомнив, что площадь трапеции равна полусумме ее оснований, умноженной на ее высоту, мы можем высказать следующим образом правило вычисления площади трапеции:

п л о щ а д ь т р а п е ц и и р а в н а е е с р е д н е й л и н и и, у м н о ж е н н о й н а в ы с о т у.

Повторительные вопросы к §§ 57 и 58

Что называется средней линией треугольника? – Каким свойством она обладает? – Как разделить данный отрезок на несколько равных частей? – Начертите какой-нибудь отрезок и разделите его на 3 равные части. – Разделите взятый вами отрезок на 7 равных частей. – Что называется средней линией трапеции? – Каким свойством она обладает? – Как можно вычислить площадь трапеции, если известны ее высота и средняя линии?

Применения

66. Фигура АВCD (черт. 164) ограничена прямой AD , двумя перпендикулярами АВ и CD и кривой ВС . Чтобы определить ее площадь, отрезок AD разделен на 5 равных частей, и из середины этих отрезков 1, 2, 3, 4, 5 восстановлены перпендикуляры к AD . Длина отрезка AD = 80 см; длины перпендикуляров: в точке 1 – 28 см, в 2 – 31 см, в.3 – 31,5 см, в 4 -32 см, в 5 – 34 см. Найти площадь АВСD .

Р е ш е н и е. Площадь первой слева полосы = 28 16 = = 448 кв. см, второй – 31 16 = = 496 кв. см, третьей – 31,5 16 = = 504кв. см, четвертой – 32 16 = 512 кв. см, пятой – 34 16 = 544 кв. см. Искомая площадь = 2 500 кв. см.

Мы знаем, что сумма углов у всех треугольников одна и та же (180°). Рассмотрим теперь, одинакова ли сумма углов у всех четырехугольников, у всех пятиугольников – вообще у всех «одноименных» многоугольников.

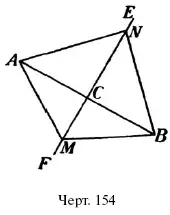
Для примера возьмем ш е с т и у г о л ь н и к (черт. 165). Проведем из какой-нибудь его вершины, напр., из A , диагонали к прочим вершинам. Мы разобьем этим наш шестиугольник на 4 треугольника. Сумма углов каждого из них 180°, а всех четырех вместе-180° 4. Но это и есть, как легко понять, сумма всех углов нашего шестиугольника.

Каковы бы ни были форма и размеры шестиугольника, он разбивается на 4 треугольника, и следовательно, сумма углов всякого шестиугольника = 180° 4 = 720°.

Если бы вместо шестиугольника, мы взяли многоугольник с другим числом сторон, например, девяти-угольник, то разбили бы его диагоналями не на 4, а на 7 треугольников; поэтому сумма углов всякого девяти-угольника равна 180° 7= 1260°.

Таким же образом найдем, что сумма углов всякого четырехугольника 180° 2 = 360°, пятиугольника 180° 3 = 540° и т. д.

Нетрудно подметить общее правило: с у м м а у г л о в в с я к о г о м н о г о у г о л ь н и к а р а в н а 180° у м н о ж е н н ы м н а ч и с л о е г о с т о р о н б е з д в у х.

Многоугольник, у которого все углы и все стороны одинаковы называются п р а в и л ь н ы м.

Величину каждого угла правильного многоугольника легко вычислить, раз мы умеем вычислять сумму всех этих углов и знаем, что они одинаковы. Например, каждый угол правильного пятиугольника равен 540°/5= 108°,

правильного шестиугольника равен 720°/6= 120°, и т. д.

Применения

67. Как убедиться, что шестиугольными плитками можно покрыть пол сплошь, без промежутков?

Р е ш е н и е. Сумма углов правильного шестиугольника равна 180° [6 – 2] = 720°, и следовательно, каждый из внутрених углов = 720°/6 =120°.Так как сумма углов, расположенных вокруг общей вершины, равна 360°, то разделив 360: 120, узнаем, что, углы трех соседних плиток, должны плотно примкнуть друг к другу.

68. Можно ли сплошь покрыть пол восьмиугольными плитками?

Решение. Внутренний угол правильного восьмиугольника = 180°[8–2]/ 8 = 125°. Так как этот угол не содержится в 360° целое число раз то покрыть такими плитками пол с п л о ш ь нельзя.

На практике нередко возникает надобность разыскать центр данной окружности или дуги. Покажем, как это делается.

Пусть требуется разыскать центр дуги, изображенной на чертеже 167. Возьмем на ней две произвольные точки, – напр. А и В (черт. 168). Центр круга должен быть, конечно, одинаково удален от каждой из них. А мы знаем, что все точки, одинаково удаленные от двух данных точек, расположены на перпендикуляре, проведенном через середину отрезка, соединяющего эти две точки (§ 55). Проведя этот перпендикуляр, получаем прямую MN (черт. 169), на которой и должен находиться искомый центр дуги. Чтобы узнать, какая именно, из точек этой прямой есть центр дуги, мы избираем на той же дуге другую пару точек, – например, С и Р (черт. 170) и, прилагая к ним те же рассуждения, проводим перпендикуляр LК к середине соединяющей их прямой. Точка О пересечения обоих перпендикуляров и есть искомый центр дуги.