Яков Перельман - Живой учебник геометрии

к а ж д а я т о ч к а п е р п е н д и к у л я р а, п р о в е д е н н о г о ч е р е з с е р е д и н у о т р е з к а, о д и н а к о в о

у д а л е н а о т к о н ц о в э т о г о о т р е з к а.

Другое следствие § 54 дает нам полезный признак равенства прямоугольных треугольников:

п р я м о у г о л ь н ы е т р е у г о л ь н и к и р а в н ы п о г и п о т е н у з е и к а т е т у.

Чтобы убедиться в этом, приложим друг к другу сравниваемые треугольники равными катетами (черт. 136). Тогда гипотенузы, как равные наклонные, должны иметь равные проекции, т. е. другие катеты этих треугольников должны быть равны. Значит, треугольники равны ( ССС ).

Повторительные вопросы к §§ 54–55

Покажите на чертеже, что называется наклонной линией, основанием перпендикуляра, основанием наклонной, проекцией. – Что длиннее: перпендикуляр или наклонная? – Что называется расстоянием от точки до прямой линии? – Каково соотношение между длиною наклонных в случае равенства проекций? – Каким свойством обладает прямая, проведенная перпендикулярно к отрезку через его середину? – Перечислите все известные вам признаки равенства прямоугольных треугольников.

Применения

62. Извилистый ручей протекает между двумя селениями. Как разыскать все места ручья, одинаково ударенные от обоих селений?

Р е ш е н и е. Соединив селения прямой линией, провешивают через ее середину перпендикуляр. Все точки пересечения этого перпендикуляра с ручьем и будут искомые.

63. Где надо поместить фонарь внутри треугольного участка, чтобы все углы «его были освещены одинаково?

Р е ш е н и е. Искомая точка должна быть одинаково удалена от всех вершин треугольника. Сначала найдем все те точки, которые одинаково отстоят от двух вершин: для этого проведем перпендикуляр через середину одной. стороны треугольника. Затем проведем перпендикуляр через середину другой стороны: на нем расположены все точки, равноудаленные от двух других вершин. Искомая точка лежит на пересечении обоих перпендикуляров.

Предварительное упражнение

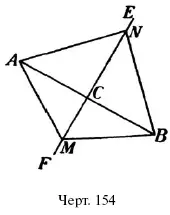
В треугольнике АВС (черт. 155) точка D есть середина А В , а прямая EF параллельна АВ . Докажите: 1) что треугольник FCE = треугольнику DBE ; 2) что фигура ADEF – параллелограмм.

Средней линией треугольника называется прямая, соединяющая середины двух его сторон ( DE на черт. 155). Этот отрезок обладает следующими свойствами:

с р е д н я я л и н и я т р е у г о л ь н и к а п а р а л л е л ь н а п р о т и в о л е ж а щ е й с т о р о н е и р а в н а е е

п о л о в и н е.

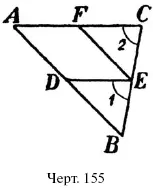
Удостоверимся в этом. Пусть в треугольнике АBС (черт 155) прямая DE соединяет середины сторон; покажем, что она параллельна стороне АС и равна ее половине. Для этого через точку Е проведем EF параллельно АВ . Треугольники DBE и FEC равны (почему?), поэтому уг. 1 = уг. 2, и значит, DE параллельно АС ; кроме того DE = FC A так как четырехугольник ADEF есть параллелограмм (почему?), то

DE = AF . Итак, DE = FC = AF = ? AC .

Мы умеем с помощью циркуля и линейки делить отрезок только на 2, на 4, на 8 и т. д. число равных частей (§ 21). Укажем теперь способ делить отрезок на любое число равных частей.

Пусть потребуется отрезок АВ (черт. 156) разделить на 5 равных частей. Проведем от одного конца этого отрезка, например, от В, под произвольным углом прямую ВС. На этой прямой отложи от конца В пять раз какой-нибудь отрезок; получим точки 1, 2, 3, 4, 5. Последнюю точку 5 соединим с концом А данного отрезка и ч через точ-ки1, 2, 3, 4 проведем прямые, параллельные прямой A 5. Можно указать, что эти прямые разделят отрезок АB на 5 равных частей в точках I, II, III, IV .

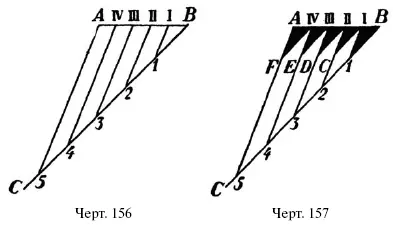
Для доказательства проведем через точки I, II, III,IV прямые, параллельные ВC (черт. 157). Получим треугольники В 1I, I C II, II D III, III Е IV, IV FА , у которых В —I, I–II, II–III, III–IV, IV— A равны между собою (потому что каждая из них, кроме 1–1, равна противоположной стороне параллелограмма, а В- 1, В -2, 2–3, 3–4, 4–5 равны друг другу). Из равенства же указанных треугольников ( СУС ) вытекает равенство отрезков B -I, 1-11, II–III, III–IV, IV–V.

Применения

Н о н и у с. Ш т а н г е н ц и р к у л ь

Умея делить прямолинейные отрезки на любое число частей, можно изготовить приспособление, полезное для точных измерений – так называемый «нониус».

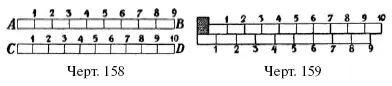
Для примера рассмотрим следующий простейший нониус. Полоску AВ (масштаб, черт. 158) длиною в 9 см разделим на 10 равных частей; по 0,9 см каждая; получим полоску CD (нониус). Пусть теперь требуется измерить длину небольшого предмета М. Прикладываем его к полоскам АВ и CD, как показывает черт. 159, и замечаем, какие деления обеих полосок совпадают. Предположим, что совпали 6-е деления. Это показывает, что длина предмета равна разнице между 6-ю делениями масштаба ПАВ и 6-ю делениями нониуса. Но 6 делений полоски АВ = 6 см, а 6 делений нониуса = 6 0,9 = 5,4 см. Следовательно, длина предмета равна 6 – 5,4 = 0,6 см. Вообще, длина измеряемого предмета равна стольким десятым долям деления масштаба, сколько единиц в совпадающих делениях масштаба и нониуса.

Если бы мы для изготовления нониуса взяли не 9 сантиметров, а 9 миллиметров, и разделили их общую длину на 10 равных частей, то разность между одним делением масштаба и одним делением нониуса равнялась бы 0,01 см. Следовательно, помощью такого нониуса мы могли бы измерять мелкие предметы с точностью до 0,1 миллиметра.

Нониус обычно применяется в форме так наз. «штангенциркуля», употребляемого для точного измерения мелких предметов. Иногда нониусом снабжается и «микрометр» – инструмент для точного измерения толщины.

Сходным образом может быть устроен нониус для точного измерения дуг. Если 9 градусных делений разделить на 10 частей, то так устроенный нониус позволит измерять дуги с точностью до 0,1 градуса, т. е. до 6.

64. На черт. 160 показано, как можно воспользоваться метром, чтобы разделить ширину доски на равные части. На чем этот способ основан?