Ю. Щербакова - Начертательная геометрия: конспект лекций

Для получения эпюра точки А, которая состоит из трех проекций а, а а , необходимо разрезать трехгранник, образующийся всеми плоскостями, вдоль оси у (рис. 15б) и совместить все эти плоскости с плоскостью фронтальной проекции. Горизонтальную плоскость необходимо вращать около оси х , а профильную плоскость – около оси z в направлении, указанном на рисунке 15 стрелкой.

На рисунке 16 изображено положение проекций а, а́ и а́́ точки А , полученное в результате совмещения всех трех плоскостей с плоскостью чертежа.

В результате разреза ось у встречается на эпюре в двух различных местах. На горизонтальной плоскости (рис. 16) она принимает вертикальное положение (перпендикулярно оси х ), а на профильной плоскости – горизонтальное (перпендикулярно оси z ).

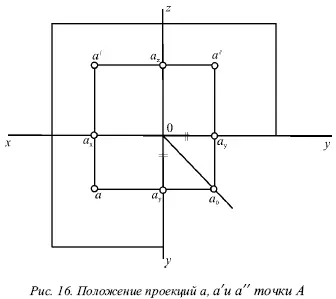
На рисунке 16 три проекции а, а́ и а́́ точки А имеют на эпюре строго определенное положение и подчинены однозначным условиям:

1) горизонтальная и фронтальная проекции а и а́ всегда должны располагаться на одной вертикальной прямой, перпендикулярной оси х ;

2) фронтальная и профильная проекции а́ и а́́ всегда должны располагаться на одной горизонтальной прямой, перпендикулярной оси z ;

3) при проведении через горизонтальную проекцию а горизонтальной прямой, а через профильную проекцию а́́ – вертикальной прямой построенные прямые обязательно пересекутся на биссектрисе угла между осями проекций, так как фигура Оа у а 0 а н– квадрат.

При выполнении построения трех проекций точки нужно проверять выполняемость всех трех условий для каждой точки.

Положение точки в пространстве может быть определено с помощью трех чисел, называемых ее координатами. Каждой координате соответствует расстояние точки от какой-нибудь плоскости проекций.

Расстояние определяемой точки А до профильной плоскости является координатой х , при этом х = а˝А (рис. 15), расстояние до фронтальной плоскости – координатой у, причем у = а́А , а расстояние до горизонтальной плоскости – координатой z , при этом z = aA .

На рисунке 15 точка А занимает ширину прямоугольного параллелепипеда, и измерения этого параллелепипеда соответствуют координатам этой точки, т. е., каждая из координат представлена на рисунке 15 четыре раза, т. е.:

х = а˝А = Оа х= а уа = a zá;

y = а́А = Оа y= а xа = а zа˝;

z = aA = Oa z= а xа́ = а yа˝.

На эпюре (рис. 16) координаты х и z встречаются по три раза:

х = а zа ́= Оа x= а yа,

z = а xá = Oa z= а yа˝.

Все отрезки, которые соответствуют координате х (или z ), являются параллельными между собой. Координата у два раза представлена осью, расположенной вертикально:

y = Оа у= а ха

и два раза – расположенной горизонтально:

у = Оа у= а zа˝.

Данное различие появилось из-за того, что ось у присутствует на эпюре в двух различных положениях.

Следует учесть, что положение каждой проекции определяется на эпюре только двумя координатами, а именно:

1) горизонтальной – координатами х и у ,

2) фронтальной – координатами x и z ,

3) профильной – координатами у и z .

Используя координаты х, у и z , можно построить проекции точки на эпюре.

Если точка А задается координатами, их запись определяется так: А ( х; у; z ).

При построении проекций точки А нужно проверять выполняемость следующих условий:

1) горизонтальная и фронтальная проекции а и а́ должны располагаться на одном перпендикуляре к оси х , так как имеют общую координату х ;

2) фронтальная и профильная проекции а́ и а˝ должны располагаться на одном перпендикуляре к оси z , так как имеют общую координату z ;

3) горизонтальная проекция а так же удалена от оси х , как и профильная проекция а удалена от оси z , так как проекции а́ и а˝ имеют общую координату у .

В случае, если точка лежит в любой из плоскостей проекций, то одна из ее координат равна нулю.

Когда точка лежит на оси проекций, две ее координаты равны нулю.

Если точка лежит в начале координат, все три ее координаты равны нулю.

Для определения прямой необходимы две точки. Точку определяют две проекции на горизонтальную и фронтальную плоскости, т. е. прямая определяется с помощью проекций двух своих точек на горизонтальной и фронтальной плоскостях.

На рисунке 17 показаны проекции ( а и á, b и b́ ) двух точек А и В. С их помощью определяется положение некоторой прямой АВ . При соединении одноименных проекций этих точек (т. е. а и b, а́ и b́ ) можно получить проекции аb и а́b́ прямой АВ.

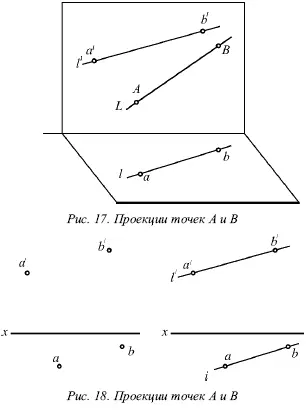
На рисунке 18 показаны проекции обеих точек, а на рисунке 19 – проекции проходящей через них прямой линии.

Если проекции прямой определяются проекциями двух ее точек, то они обозначаются двумя рядом поставленными латинскими буквами, соответствующими обозначениям проекций точек, взятых на прямой: со штрихами для обозначения фронтальной проекции прямой или без штрихов – для горизонтальной проекции.

Если рассматривать не отдельные точки прямой, а ее проекции в целом, то данные проекции обозначаются цифрами.

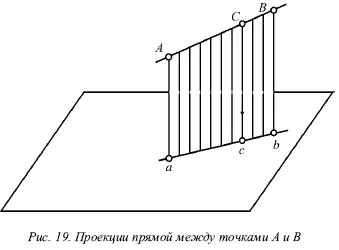
Если некоторая точка С лежит на прямой АВ , ее проекции с и с́ находятся на одноименных проекциях прямой ab и а́b́ . Данную ситуацию поясняет рисунок 19.

След прямой– это точка пересечения ее с некоторой плоскостью или поверхностью (рис. 20).

Горизонтальным следом прямойназывается некоторая точка H , в которой прямая встречается с горизонтальной плоскостью, а фронтальным– точка V , в которой данная прямая встречается с фронтальной плоскостью (рис. 20).

На рисунке 21а изображен горизонтальный след прямой, а ее фронтальный след, – на рисунке 21б.

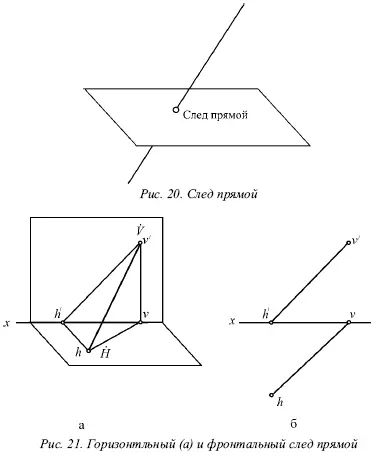
Иногда также рассматривается профильный след прямой, W – точка пересечения прямой с профильной плоскостью.

Горизонтальный след находится в горизонтальной плоскости, т. е. его горизонтальная проекция h совпадает с этим следом, а фронтальная h́ лежит на оси х. Фронтальный след лежит во фронтальной плоскости, поэтому его фронтальная проекция ν́ совпадает с ним же, а горизонтальная v лежит на оси х.