Ю. Щербакова - Начертательная геометрия: конспект лекций

На основании законов стереометрии плоскость определяется, когда известны принадлежащие ей:

1) три точки, не лежащие на одной прямой;

2) прямая и точка, не находящаяся на этой прямой;

3) две пересекающиеся прямые;

4) две параллельные прямые.

Итак, плоскость будет считаться заданной, если имеется на эпюре одна из перечисленных выше комбинаций элементов, определяющих данную плоскость (рис. 35 случаи 1, 2, 3, 4).

Все четыре способа задания плоскости равнозначны, так как легко имея одну комбинацию элементов, изображенную на рисунке 35 перейти к любой другой.

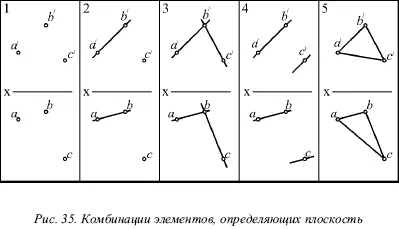
Если соединить одноименные проекции трех точек А, В и С , определяющих данную плоскость (рис. 35, случай 5), можно получить проекции треугольника ABC , лежащего в этой плоскости. Способ изображения плоскости в виде треугольника, не является принципиально новым, но обладает по сравнению с остальными четырьмя случаями большей наглядностью.

След плоскости Р – это линия пересечения ее с данной плоскостью или поверхностью (рис. 36).

Линию пересечения плоскости Р с горизонтальной плоскостью называют горизонтальным следоми обозначают P h, а линию пересечения с фронтальной плоскостью – фронтальным следоми обозначают Р v(рис. 37).

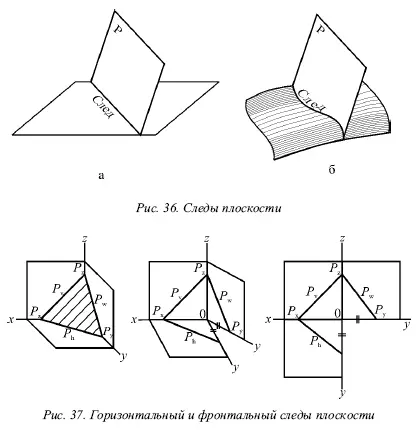
Иногда применяется и профильный след P w– линия пересечения данной плоскости с профильной плоскостью.

Точки, в которых пересекается плоскость Р с осями проекций, называют точками схода следов. Р х– точка схода следов на оси х, P у– на оси у , а Р z– на оси z (рис. 37). в точке Р пересекаются следы P hи P vи т. д.

Следы P hи P vплоскости Р являются прямыми, которые и лежат на горизонтальной и фронтальной плоскостях. Они имеют по одной из своих проекций, которые совпадают с осью х : горизонтальный след P h– фронтальную, а фронтальный P v– горизонтальную проекции.

Любую плоскость Р можно задать на эпюре с помощью указания положения двух ее следов – горизонтального и фронтального (рис. 38).

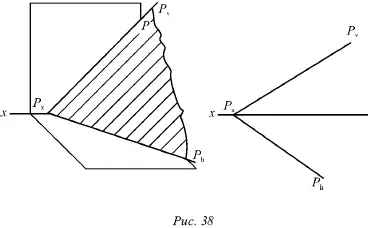
Следы P hи P vчаще всего изображаются парой пересекающихся или параллельных прямых и поэтому могут определять положение плоскости в пространстве.

Прямая принадлежит плоскости Р в том случае, если любые две ее точки лежат в данной плоскости.

Например, если следы прямой лежат на одноименных следах плоскости, то прямая лежит в этой плоскости (рис. 39).

Рассмотрим построение прямой, лежащей в данной плоскости Р .

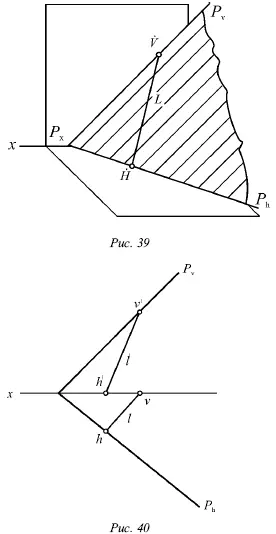
Первый способ.Возьмем на следах P hи P vпо одной точке (рис. 40) и рассмотрим их как следы искомой прямой.

Рассматривая следы прямой, легко построить ее проекции.

Второй способ.Одну проекцию прямой, например горизонтальную 1, можно провести (рис. 40). Точки ее пересечения со следом P hи осью х определят горизонтальные проекции h и v следов искомой прямой. Если соединить прямой фронтальные проекции h́ и v́ следов, можно получить фронтальную проекцию 1́.

Среди прямых, которые лежат в некоторой плоскости, можно выделить два класса прямых, играющих большую роль при решении всевозможных задач. Это прямые, которые называют горизонталямии фронталями.

Горизонталь плоскости Р (рис. 41) – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости. Горизонталь как прямая, параллельная горизонтальной плоскости, имеет фронтальную проекцию ѓ , параллельную оси х .

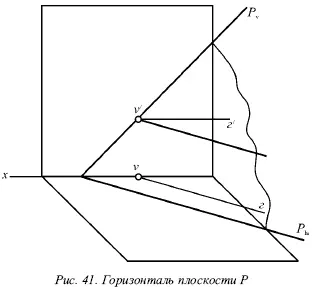
Три прямые – горизонталь Г , ее горизонтальная проекция г и горизонтальный след P hплоскости Р – параллельны (рис. 42).

Действительно, горизонталь является прямой, параллельной горизонтальной плоскости, и поэтому не имеет горизонтального следа P h, лежащего с ней в одной плоскости. При этом горизонталь Г не может пересечь свою горизонтальную проекцию г . В противном случае в этой точке пересечения она встречала бы горизонтальную плоскость, что противоречит определению, т. е. все три прямые Г , г и P hпараллельны.

Любая из плоскостей имеет множество горизонталей. Все горизонтали этой плоскости параллельны друг другу вследствие того, что все они параллельны прямой P h.

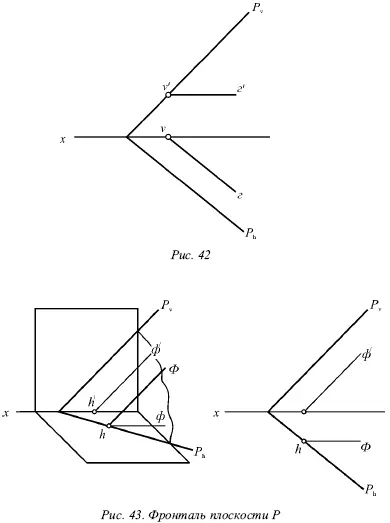
Фронталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости (рис. 43).

Фронталь является прямой, параллельной фронтальной плоскости, и ее горизонтальная проекция ф параллельна оси х .

Фронталь Ф, ее фронтальная проекция ф́ и фронтальный след P vвзаимно параллельны. У каждой плоскости есть бесчисленное множество фронталей. Все фронтали данной плоскости параллельны, за исключением плоскости, параллельной фронтальной плоскости.

Если необходимо построить некоторую точку в данной плоскости Р , то нужно предварительно провести в этой плоскости одну из прямых и на ней взять искомую точку.

Если задача обратная, т. е. необходимо узнать, лежит ли данная точка в плоскости Р , то нужно провести через эту точку какую-нибудь прямую, лежащую в этой плоскости. Если такую прямую провести нельзя, то исследуемая точка М не лежит в плоскости Р .

Часто в качестве вспомогательной прямой применяют горизонталь или фронталь, хотя можно применять и прямые общего положения.

Покажем построение в плоскости Р произвольной точки (рис. 44).

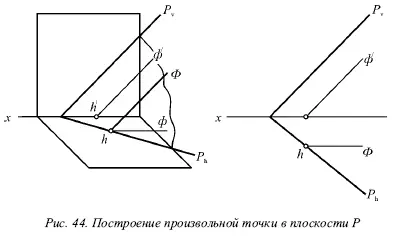
Для выполнения задания необходимо провести любую горизонталь Г этой плоскости и на ней выбрать некоторую точку М . Данная точка принадлежит плоскости, следовательно, задача выполнена.