Ю. Щербакова - Начертательная геометрия: конспект лекций

Прямое утверждение справедливо во всех случаях без исключения. Обратное же утверждение неприменимо в том случае, если хотя бы одна из прямых профильная.

Когда прямые параллельны, на эпюре их одноименные проекции параллельны (рис. 28).

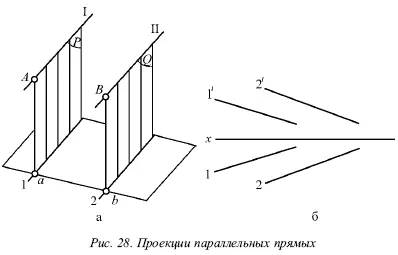
На самом деле, плоскости Р и Q , проецирующие прямые I и II на горизонтальную плоскость, параллельны, так как в каждой из этих плоскостей можно указать две пересекающиеся прямые, параллельные двум пересекающимся прямым второй плоскости, т. е. прямая I параллельна прямой II, и проектирующий луч Аа параллелен лучу Вb . Но две параллельные плоскости Р и Q пересекут горизонтальную плоскость. В результате этого образуются две параллельные прямые 1 и 2, т. е. горизонтальные проекции прямых I и II параллельны между собой.

Аналогично можно доказать, что и любые другие одноименные проекции обеих прямых также будут параллельны друг другу.

Верно и обратное утверждение: прямые параллельны, если на эпюре их одноименные проекции параллельны.

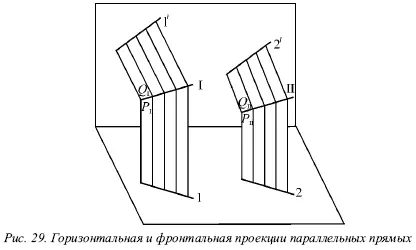
Если известно, что горизонтальные и фронтальные проекции прямых I и II параллельны, будет справедливо следующее: 1 || 2 и 1́|| 2́ (рис. 29).

В этом случае можно сказать, что плоскости Р Iи Р II, проецирующие прямые I и II на горизонтальную плоскость, параллельны, так как в этих плоскостях можно указать по паре пересекающихся соответственно параллельных прямых (прямые 1 и 2 и проецирующие лучи). Аналогично плоскости Q Iи Q IIбудут параллельны.

Прямая I находится в пересечении плоскостей Р Iи Q I, а прямая II – в пересечении плоскостей Р IIQ II. Отсюда получаем, что прямая I параллельна плоскости Р II, потому что находится в плоскости, ей параллельной. Однако прямая I параллельна и плоскости Q II. Поэтому прямая I параллельна линии пересечения плоскостей Р IIи Q II, т. е. прямой II.

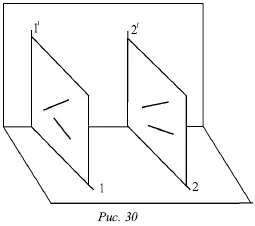
Доказательство обратного утверждения не имеет смысла для профильных прямых. Это объясняется тем, что тогда вместо двух плоскостей, проецирующих прямую на горизонтальную и фронтальную плоскости, существует только одна, дважды проецирующая плоскость (рис. 30).

Видно, что вне зависимости от расположения двух профильных прямых I и II в пространстве их горизонтальные и фронтальные проекции всегда параллельны (или сливаются).

Прямые будут являться скрещивающимися, если они не параллельны и не пересекаются. Это вытекает из того, что возможны только три случая взаимного расположения прямых.

Для скрещивающихся прямых справедливы утверждения:

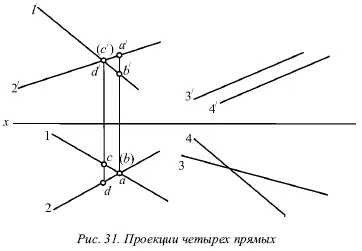
1) точки пересечения одноименных проекций на горизонтальной и фронтальной плоскостях не лежат на одном перпендикуляре к оси х (прямые I и II на рис. 31).

2) хотя бы в одной паре одноименные проекции не параллельны (прямые III и IV на рис. 31).

Рисунок 31 показывает проекции четырех прямых, любая пара из которых скрещивается.

Как и в рассмотренных ранее случаях, обратное утверждение для скрещивающихся прямых несправедливо при условии, что хотя бы одна из прямых является профильной.

Рассмотрим теорему: если одна сторона прямого угла параллельна плоскости проекций (или лежит в ней), то прямой угол проецируется на эту плоскость без искажения.

Приведем доказательство для прямого угла ABC , одна сторона которого ВС параллельна горизонтальной плоскости (рис. 32).

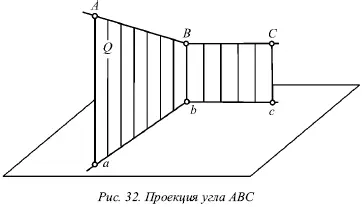
Плоскость, в которой находится сторона угла АВ и ее проекция ab , перпендикулярна горизонтальной плоскости, так как содержит перпендикуляр Вb к этой плоскости. Прямая ВС перпендикулярна плоскости Q вследствие ее перпендикулярности двум пересекающимся прямым этой плоскости ( АВ и Вb ). Прямая bc параллельна ВС , т. е. она также перпендикулярна Q , а значит и прямой ab , которая лежит в ней.

Ясно, что если на эпюре одна пара одноименных проекций двух прямых перпендикулярна, а одна из двух остальных проекций параллельна оси х , то такие прямые образуют в пространстве прямой угол.

Предположим, что ab ⊥ bc, b́с́ || x.

Это показано на рисунке 33.

Можно провести через проекцию аb плоскость Q , проектирующую прямую АВ на горизонтальную плоскость (рис. 33). Проекция bсперпендикулярна плоскости Q вследствие того, что она перпендикулярна двум прямым этой плоскости, т. е. проекции аb (по условию), и проецирующему лучу Вb как перпендикуляру горизонтальной плоскости.

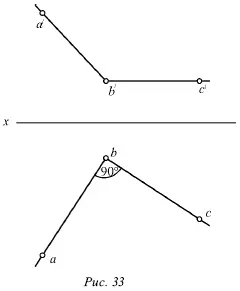
Прямая ВС является параллельной горизонтальной плоскости, так как ее фронтальная проекция bс параллельна оси х , поэтому она параллельна своей горизонтальной проекции, т. е. справедливо выражение ВС || bс . Следовательно, прямая ВС перпендикулярна плоскости Q и поэтому перпендикулярна прямой АВ вне зависимости от ее положения в плоскости Q .

Через некоторую точку М можно провести огромное количество прямых, которые перпендикулярны данной прямой АВ . Они образуют целую плоскость Р , перпендикулярную АВ (рис. 34).

Из всех перпендикулярных прямых, которые при этом образуются, только одна пересекает данную прямую. Это прямая MN , которая проходит через точку N пересечения прямой АВ и плоскости Р .

Под перпендикуляром к прямой подразумевается прямая, не только перпендикулярная данной прямой, но и пересекающая в отличие от просто перпендикулярных скрещивающиеся прямые.

Прямой угол между скрещивающимися прямыми проецируется на данную плоскость проекций без искажения, если одна из прямых параллельна этой плоскости или лежит в ней.

Для произвольно расположенной плоскости проекции ее точек заполняют все три плоскости проекций. Поэтому не имеет смысла говорить о проекции всей плоскости целиком, нужно рассматривать лишь проекции таких элементов плоскости, которые ее определяют.