Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> restart: with(PDEtools):

> PDE := x*diff(f(x, y), y) - diff(f(x,y),x)=f(x,y;^2*g(x)/h(y);

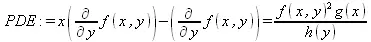
> ans := pdsolve(PDE);

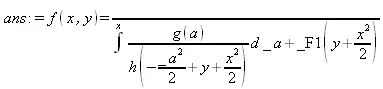
> PDE := S(x,y)*diff(S(x,y),y,x) + diff(S(x,y),x)*diff(S(x,y),y) = 1;

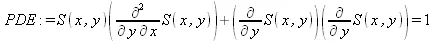
> struc := pdsolve(PDE, HINT=f(x)*g(y));

> build(struc);

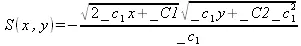
> pdsolve(PDE,HINT=P(x,y)^(1/2));

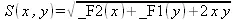
> PDE := diff(f(x,y,z), x) + diff(f(x,y,z), у)^2 = f(x,y,z)+z;

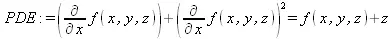
> pdsolve(PDE, HINT=strip);

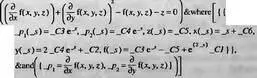
> myPDEsystem := [-y*diff(f(x,у,z,t),x) +

z^2*diff(f(x,y,z,t),z) + 3*t*z*diff(f(x,y,z,t),t) - 3*t^2-4*f(x,y,z,t)*z = 0,

-y*diff(f(x, y, z, t), y) - z*diff(f(x,y,z,t),z) -

t*diff(f(x,y,z,t), t) + f(x,y,z,t) = 0,

-x*diff(f(x, y, z, t), y) - diff(f(x,y,z,t),z)=0]:

for _eq in myPDEsystem do

_eq;

od;

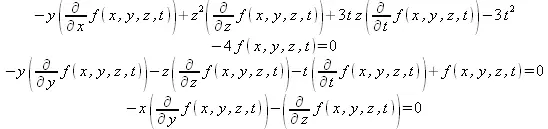
> sol := pdsolve(myPDEsystem);

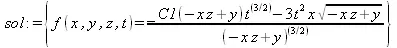
Обратите внимание на то, что в последнем примере из справки решена система дифференциальных уравнений в частных производных.

Одна из важнейших функций пакета DEtools — DEtools[PDEplot] — служит для построения графиков решения систем с квазилинейными дифференциальными уравнениями первого порядка в частных производных. Эта функция используется в следующем виде:

PCEplot(pdiffeq, var, i_curve, srange, o)

PDEplot(pdrffeq, var, i_curve, srange, xrange, yrange, urange, o)

Здесь помимо упоминавшихся ранее параметров используются следующие: pdiffeq — квазилинейные дифференциальные уравнения первого порядка (PDE), vars — независимая переменная и i_curve — начальные условия для параметрических кривых трехмерной поверхности. Помимо опций, указанных для функции DEplot, здесь могут использоваться следующие опции:

• animate = true, false — включение (true) или выключение (false) режима анимации графиков;

• basechar = true, false, ONLY — устанавливает показ начального условия на плоскости (х,у);

• basecolor = b_color — устанавливает цвет базовых характеристик;

• ic_assumptions — задание (в виде равенств или неравенств) ограничений на начальные условия для первых производных;

• initcolor = i_color — инициализация цвета кривой начальных условий;

• numchar = integer — залает число отрезков кривых, которое не должно быть меньше 4 (по умолчанию 20);

• numsteps = [integer1, integer2] — задает число шагов интегрирования (по умолчанию [10,10]);

• obsrange = true, false — прекращение интегрирования (true) при выходе отображаемой переменной за заданные пределы или продолжение интегрирования (false) в любом случае;

• scene=[x,y,u(x,y)] — вывод обозначений координатных осей.

С помощью параметров и опций можно задать множество возможностей для наглядной визуализации довольно сложных решений систем дифференциальных уравнений с частными производными. Следует отметить, что неправильное задание параметров ведет просто к выводу функции в строке вывода без построения графиков и нередко без сообщений об ошибках. Поэтому полезно внимательно просмотреть примеры применения этой функции — как приведенные ниже, так и в справке.

Рисунок 7.28 демонстрирует применение функции PDEplot. Этот пример из справки показывает, насколько необычным может быть решение даже простой системы дифференциальных уравнений в частных производных.

Рис. 7 28. Пример применения функции PDEplot

В данном случае решение представлено трехмерной фигурой весьма нерегулярного вида.

Другой пример использования функции PDEplot показан на рис. 7.29. Он иллюстрирует комбинированное построение графиков решения разного типа с применением функциональной закраски, реализуемой по заданной формуле с помощью опции initcolor.

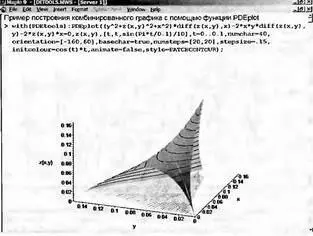
Рис. 7.29. Построение комбинированного графика с помощью функции PDEplot

Еще раз отметим, что, к сожалению, рисунки в данной книге не дают представления о цвете выводимых системой Maple графиков. Поэтому наглядность решений, видимых на экране монитора, существенно выше.

Многие системы (например, нелинейные оптические резонаторы, лазерные устройства и др.) описываются системами из более чем двух нелинейных дифференциальных уравнений. Колебания в таких системах нередко носят сложный нестационарный, а порою даже хаотический характер. Примером этого может служить анализ переходных процессов в системе, описываемой тремя дифференциальными уравнениями и представленной на рис. 7.30.

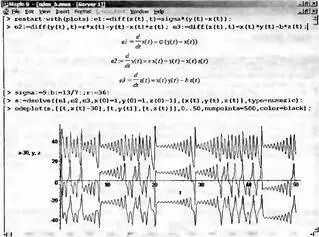
Рис. 7.30. Пример решения системы из трех нелинейных дифференциальных уравнений, создающей колебания сложной формы

Поведение системы описывается тремя постоянными sigma, b и r, меняя которые можно получить самый различный вид временных зависимостей x(t), y(t) и z(t). Даже на ограниченном промежутке времени эти зависимости имеют весьма сложный и почти непредсказуемый характер и далеки от периодических колебаний. Нередко в них проглядывает фрактальный характер.

Функция odeplot позволяет получать не только графики временных зависимостей, но и фазовые портреты колебаний. Рисунок 7.31 показывает построение фазового портрета в плоскости (x, y).

Рис. 7.31. Фазовый портрет колебаний на плоскости (х, у)

Нетрудно заметить, что фазовый портрет отчетливо выделяет два фокуса, которые соответствуют слабым осцилляциям нарастающих почти гармонических колебаний, время от времени повторяющимся. В целом же фазовый портрет колебаний оказывается довольно запутанным и хорошо иллюстрирует развитие нестационарных компонент колебаний.