Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Еще более интересный пример решения дифференциального уравнения представлен на рис. 7.20. Здесь построены фазовые портреты для асимптотических решений.

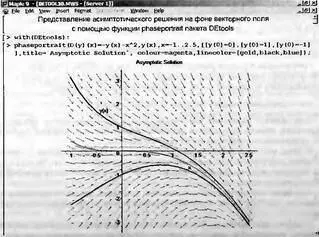
Рис. 7.20. Построение асимптотического решения на фоне графика векторного поля

В целом надо отметить, что возможности визуализации решений дифференциальных уравнений с помощью системы Maple весьма велики и приведенные выше примеры лишь частично иллюстрируют сказанное.

Maple 9.5 существенно доработан по части решения дифференциальных уравнений (ДУ) и систем с ДУ. Эта доработка, прежде всего, направлена на получение верных решений как можно большего числа ДУ разных классов и систем с ДУ. В частности расширен круг нелинейных дифференциальных уравнений, для которых система Maple 9.5 способна дать аналитические решения.

Весь арсенал средств решения ДУ и методика их применения вполне заслуживают отражения в отдельной большой книге. Мы ограничимся описанием только трех средств системы Maple — проверки ДУ на автономность, углубленным анализом решения с помощью контроля уровня выхода и получением приближенного полиномиального аналитического решения.

Одиночное дифференциальное уравнение или система дифференциальных уравнений называется автономной, если их правая часть явно не зависит от независимой переменной. Для автономных дифференциальных уравнений или систем при построении графиков решений функцией DEplot не обязательно задавать начальные условия, но нужно указывать диапазон изменения искомых переменных.

Для проверки уравнений (или систем) на автономность используется функция

autonomous(des,vars, ivar)

где des — заданное дифференциальное уравнение или (в виде списка) система дифференциальных уравнений, vars — зависимые переменные и ivar — независимая переменная. Если система автономна, то эта функция возвращает true, в противном случае false.

Примеры:

> dif1:=diff(х(t),t)=x(t)*(1-y(t));

dif2:=diff(y(t),t)=.3*y(t)*(x(t)-1);

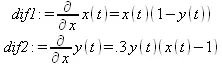
> autonomous({dif1,dif2),[x(t),y(t)],t);

> autonomous(diff(x(t),t)=sin(t),x,t);

В первом случае система дифференциальных уравнений (модель Лотки-Вольтерра) автономна, а во втором случае дифференциальное уравнение не автономно.

Для углубленного анализа аналитического решения ДУ (или системы ДУ) можно использовать специальную возможность управления уровнем вывода решения с помощью системной переменной infolevel(dsolve):=level. Значение level=all дает обычный вывод решения без комментариев, уровень 1 зарезервирован для информации, которую может сообщить пользователь, уровень 2 или 3 дает более детальный вывод (включая сообщения об использованном алгоритме и технике решения) и, наконец, уровни 4 и 5 дают наиболее детальную информацию (если таковая есть в дополнение к той информации, которую дает уровень 2 или 3).

Приведем пример аналитического решения ДУ третьего порядка с контролем уровня вывода решения (файл deil):

> myDE:= x^2 * diff(y(х),х,х,х) - 2*(n+1)*x*diff(y(х), х, х) + (а*х^2+6*n)*diff(y(х),х)-2*а*х-y(х) = 0;

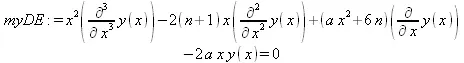
> infolevel[dsolve] := all: dsolve(myDE);

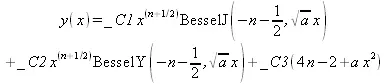
> infolevel[dsolve] := 1:dsolve(myDE);

<- No Liouvillian solutions exists

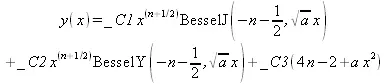
> infolevel[dsolve] := 3:dsolve(myDE); Methods for third order ODEs:

-- Trying classification methods --

trying a quadrature

checking if the LODE has constant coefficients

checking if the LODE is of Euler type

trying high order exact linear fully integrable

trying to convert to a linear ODE with constant coefficients

Equation is the LCLM of -2*x/(2*(2*n-1)/а+х^2)*y(x)+diff(y(x), x), a*y(x)-@KOD = 2*n/x*diff(y(x),x)+diff(diff(y(x),x),x)

checking if the LODE is of Euler type

-> Attemtping a differential factorization

trying exponential solutions

checking if the LODE is of Euler type 1, exponential solutions found

exponential solutions successful

<- differential factorization successful

-> Tackling the linear ODE "as given":

trying a quadrature

checking if the LODE has constant coefficients

checking if the LODE is of Euler type

trying a symmetry of the form [xi=0, eta=F(x)]

checking if the LODE is missing 'y'

-> Trying a Liouvillian solution using Kovacic's algorithm

<- No Liouvillian solutions exists

-> Trying a solution in terms of special functions:

-> Bessel

<- Bessel successful

<- special function solution successful

<- successful solving of the linear ODE "as given"

<- solving the LCLM ode successful

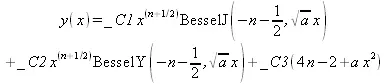
В данном случае повышение уровня вывода до 4 или 5 бесполезно, поскольку вся информация о решении сообщается уже при уровне 2 (или 3).

Во многих случаях аналитические решения даже простых ДУ оказываются весьма сложными, например, содержат специальные математические функции. При этом нередко полезна подмена такого решения другим, тоже аналитическим, но приближенным решением. Наиболее распространенным приближенным решением в этом случае может быть полиномиальное решение, то есть замена реального решения полиномом той или иной степени. При этом порядок полинома задается значением системной переменной Order, а для получения такого решения функция dsolve должна иметь параметр series.

На рис. 7.21 представлено решение ДУ третьего порядка различными методами: точное аналитическое и приближенное в виде полинома с максимальным заданным порядком 10 и 60. График дает сравнение этих решений для зависимости у(t).

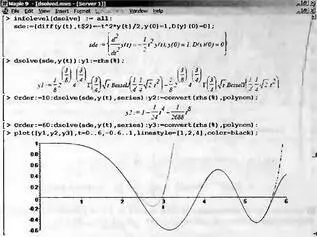
Рис. 7.21. Примеры решения ДУ третьего порядка

Дадим небольшой комментарий. Нетрудно заметить, что точное аналитическое решение весьма сложно и содержит специальные функции Бесселя и гамма-функции. При порядке полинома 8 (он несколько меньше заданного максимального) решение практически совпадает с точным до значений t<2, а при максимальном заданном порядке 60 область совпадения расширяется до значений t<5,5. Затем приближенное решение резко отходит от точного.