Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

varparam(sols,v,ivar)

находит общее решение дифференциального уравнения (или системы уравнений) sols методом вариации параметров. Параметр v задает правую часть уравнения; если он равен 0, ищется только частичное решение.

> varparam([u1(х), u2(х)[LDV4]], g(x), х);

Более подробную информацию об этих функциях читатель найдет в их справочных страницах, а также в информационном документе DEtools.mws, содержащем систематизированное описание пакета DEtools с многочисленными примерами его применения.

Средствами пакета DEtools предусмотрена работа с дифференциальными операторами DF, которые дают компактное представление производных, например (файл difop):

> restart; with(DEtools):

> df := x*2*DF^2 - x*DF + (х^2 - 1);

Данное выражение представляет собой дифференциальное уравнение второго порядка, записанное через дифференциальные операторы. С помощью функции diffop2de это уравнение можно преобразовать в обычное дифференциальное уравнение:

> diffop2de(df,y(x),[DF,x]);

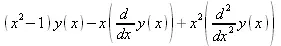
Теперь это уравнение можно решить с помощью функции dsolve :

> dsolve(%, y(x));

Уравнения с дифференциальными операторами имеет вид степенного многочлена. Поэтому с ним можно выполнять множество операций, характерных для полиномов, например факторизацию, комплектование по степеням и др. В практике инженерных и научных расчетов дифференциальные операторы применяются довольно редко. Множество примеров с ними дано в файле примеров diffop.mws.

Для обычного графического представления результатов решения дифференциальных уравнений может использоваться функция odeplot из описанного выше пакета plots. Эта функция используется в следующем виде:

odeplot(s,vars, r, о)

где s — запись (в выходной форме) дифференциального уравнения или системы дифференциальных уравнений, решаемых численно функцией dsolve, vars — переменные, r — параметр, задающий пределы решения (например, a..b) и о — необязательные дополнительные опции.

На рис. 7.11 представлен пример решения одиночного дифференциального уравнения с выводом решения у(х) с помощью функции odeplot.

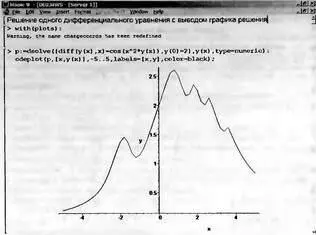
Рис. 7.11. Пример решения одиночного дифференциального уравнения

В этом примере решается дифференциальное уравнение

при у(0)=2 и х, меняющемся от -5 до 5. Левая часть уравнения записана с помощью функции вычисления производной diff. Результатом построения является график решения y(x).

В другом примере (рис. 7.12) представлено решение системы из двух нелинейных дифференциальных уравнений. Здесь с помощью функции odeplot строятся графики двух функций — y(х) и z(x).

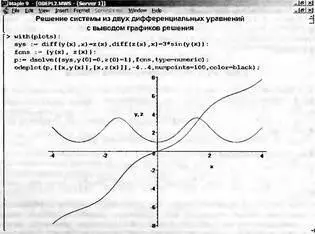
Рис. 7.12. Пример решения системы из двух дифференциальных уравнений

В этом примере решается система:

при начальных условиях y(0)=0, z(0)=1 и х, меняющемся от -4 до 4 при числе точек решения, равном 25.

Иногда решение системы из двух дифференциальных уравнений (или одного дифференциального уравнения второго порядка) представляется в виде фазового портрета — при этом по осям графика откладываются значения у(х) и z(х) при изменении х в определенных пределах. Рисунок 7.13 демонстрирует построение фазового портрета для системы, представленной выше.

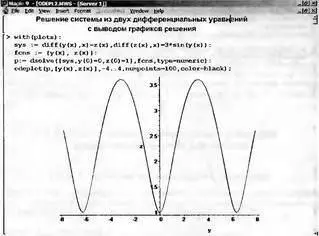
Рис. 7.13. Представление решения системы дифференциальных уравнений в виде фазового портрета

Обычное решение, как правило, более наглядно, чем фазовый портрет решения. Однако для специалистов (например, в теории колебаний) фазовый портрет порою дает больше информации, чем обычное решение. Он более трудоемок для построения, поэтому возможность Maple быстро строить фазовые портреты трудно переоценить.

Специально для решения и визуализации решений дифференциальных уравнений и систем с дифференциальными уравнениями служит инструментальный пакет DEtools. В него входит ряд функций для построения наиболее сложных и изысканных графиков решения дифференциальных уравнений. Основной из этих функций является функция DEplot.

Функция DEplot может записываться в нескольких формах:

DEplot(deqns, vars, trange, eqns)

DEplot(deqns, vars, trange, inits, eqns)

DEplot(deqns, vars, trange, yrange, xrange, eqns)

DEplot(deqns, vars, trange, inits, xrange, yrange, eqns)

Здесь deqns — список или множество, содержащее систему дифференциальных уравнений первого порядка или одиночное уравнение любого порядка; vars — зависимая переменная или список либо множество зависимых переменных; trange — область изменения независимой переменной t; inits — начальные условия для решения; yrange — область изменения для первой зависимой пере-

менной, xrange — область изменения для второй зависимой переменной; eqns — опция, записываемая в виде keyword=value. Замена имен переменных другими в данном случае недопустима.

Эта функция обеспечивает численное решение дифференциальных уравнений или их систем при одной независимой переменной t и строит графики решения. Для автономных систем эти графики строятся в виде векторного поля направлений, а для неавтономных систем — только в виде кривых решения. По умолчанию реализуется метод Рунге-Кутта 4-го порядка, что соответствует опции method=classical[rk4],

С функцией DEplot могут использоваться следующие параметры:

• arrows=type — тип стрелки векторного поля ('SMALL', 'MEDIUM', 'LARGE', 'LINE' или 'NONE');

• colour, color = arfowcolour — цвет стрелок (задается 7 способами);

• dirgrid = [integer,integer] — число линий сетки (по умолчанию [20, 20]);

• iterations = integer — количество итераций, представленное целым числом;

• linecolor, linecolor = line_info — цвет линии (задается 5 способами);