Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Цвет трехмерного графика может задаваться (как и для двумерного) параметром color=c, где с — цвет (оттенки цвета перечислялись ранее). Возможно еще два алгоритма задания цвета:

HUE — алгоритм с заданием цвета в виде color=f(x,y);

RGB — алгоритм с заданием цвета в виде color=[exprr,exprg,exprb], где выражения exprr, exprg и exprb задают относительную значимость (от 0 до 1) основных цветов (красного — exprr, зеленого — exprg и синего — exprb)

Удачный выбор углов обзора фигуры и применение функциональной окраски позволяют придать построениям трехмерных фигур весьма эффектный и реалистический вид.

Как отмечалось, вид графика трехмерной поверхности существенно зависит от выбора координатной системы. Рис. 8.11 показывает пример построения нелинейного конуса в цилиндрической системе координат. Для задания такой системы координат используется параметр coords=cylindrical.

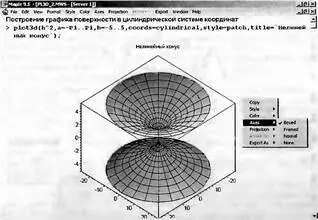
Рис. 8.11. Нелинейная цилиндрическая поверхность

При построении этой фигуры также использована цветная функциональная окраска. Кроме того, этот пример иллюстрирует вывод над рисунком титульной надписи (кстати, сделанной на русском языке).

Приведем еще один пример построения трехмерной поверхности — на этот раз в сферической системе координат (рис. 8.12). Здесь функция задана вообще элементарно просто — в виде числа 1. Но, поскольку выбрана сферическая система координат, в результате строится поверхность шара единичного радиуса. Обратите внимание на возможность построения только части сферы за счет ограничения изменения переменных координатной системы.

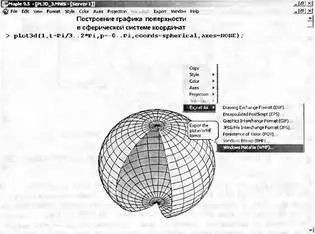
Рис. 8.12. Построение шарообразной поверхности в сферическом системе координат

Полезно просмотреть построение графиков в различных системах координат. При этом можно получить самые необычные фигуры.

На рис. 8.13 показано построение простого тороида — цилиндра, свернутого в кольцо. Здесь также использован прием удаления части фигуры, что делает ее представление более наглядным и красочным. Кроме того, введены параметры, задающие функциональную окраску.

Рисунок 8.13 дает полное и наглядное представление об этой фигуре — причем не только снаружи, но и изнутри.

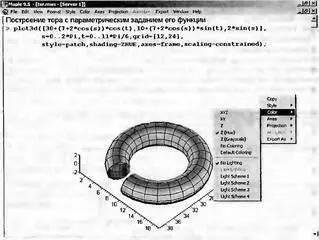
Рис. 8.13. Тор с функциональной окраской поверхности

Полезно обратить внимание на параметр масштаба scaling=constrained, явно введенную в документ рис. 8.13. Ее можно было бы и не вводить, поскольку этот параметр изначально задается по умолчанию. Она выравнивает масштабы представления фигуры по осям координат, обычно используется по умолчанию и позволяет снизить до минимума геометрические искажения фигур — тор, например, при этом виден как круглая труба, свернутая в кольцо. У таких графиков есть специфический недостаток — они занимают малую часть окна вывода.

Задание параметра scaling=unconstrained означает отказ от равного масштаба по осям. График при этом увеличивается в размерах, но становятся заметны его искажения по осям координат. В итоге он тор превращается в толстую сплющенную трубу с эллиптическим сечением (рис. 8.14).

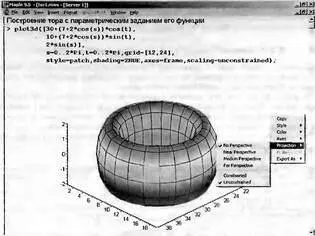
Рис. 8.14. Тор, построенный с применением значения параметра scaling=unconstrained

Весьма важным является учет углов, под которыми наблюдается трехмерная поверхность или объект. К примеру, построение рис. 8.14 неудачно в том плане, что оно не показывает наличия у тора дырки. Простейший и очень удобный способ изменить угол обзора заключается во вращении фигуры на рисунке мышью при нажатой левой кнопке. При этом можно повернуть фигуру так, что ее геометрические особенности будут отчетливо видны. Попробуйте проделать это.

В Maple есть способ явно задать углы обзора с помощью параметра orientation=[theta, phi], где theta и phi — углы, через которые задаются параметрические уравнения трехмерной фигуры или поверхности. Рисунок 8.15 дает пример такого задания фигуры, которую можно назвать «квадратным» тором.

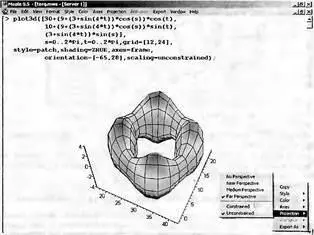
Рис. 8.15. «Квадратный» тор, представленный под заданными углами обзора

Обратите внимание, что значения заданных углов обзора повторяются в полях углов на контекстной панели инструментов. Разумеется, последние будут меняться, если начать вращать фигуру на рисунке мышью.

Параметрическое задание уравнений поверхности открывает почти неисчерпаемые возможности построения занимательных и сложных фигур самого различного вида. Приведем пару построений такого рода.

На рис. 8.16 показан тор, сечение которого имеет вид сплюснутой шестиконечной звезды. Вырез в фигуре дает прекрасный обзор ее внутренней поверхности, а цветная функциональная окраска и линии сетки, построенные с применением алгоритма удаления невидимых линий, дают весьма реалистичный вид фигуры. Замените параметр scaling=unconstrained на scaling=constrained, и вы получите тор с неискаженным сечением.

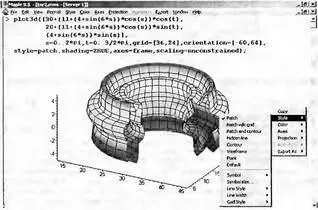
Рис. 8 16. Тор с сечением в виде шестиконечной звезды

На рис. 8.17 показан еще один тор. На этот раз он круглого сечения, но сверху к снизу имеет вид пятиконечной звезды.

Рис. 8.17. Тор круглого сечения в виде пятиконечной звезды

Быстрое (не в смысле ускорения самого построения, а лишь в смысле более быстрою задания построения графиков) построение трехмерных графиков обеспечивает функция smartplot3d.

Функция plot3d позволяет строить одновременно несколько фигур, пересекающихся в пространстве. Для этого достаточно вместо описания одной поверхности задать список описаний ряда поверхностей. При этом функция plot3d обладает уникальной возможностью — автоматически вычисляет точки пересечения фигур и показывает только видимые части поверхностей. Это создает изображения, выглядящие вполне естественно. Пример такого построения для двух функций показан на рис. 8.18.