Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

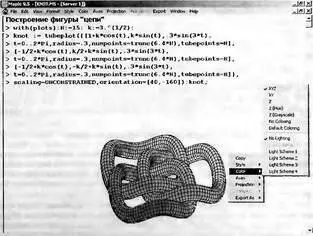
Рис. 8.29. Фигура «цепи», построенная с применением функции tubeplot

Можно долго размышлять о том, как те или иные математические закономерности описывают предметы реального мира, положенные в основу тех или иных геометрических объектов или, возможно, о гениальности людей, сумевших найти такие закономерности для многих из таких объектов. В наше время Maple открывает огромные возможности для таких людей.

Наглядность ряда графиков можно существенно увеличить, строя их в трехмерном представлении. Например, для такого построения графиков полей из векторов можно использовать графическую функцию fieldplot3d. В отличие от функции fieldplot она строит стрелки как бы в трехмерном пространстве (рис. 8.30). Возможности смены осей о оформления «ящика» графика иллюстрирует контекстное меню правой клавиши мыши, показанное на рис. 8.30.

Рис. 8.30. Построение поля в трехмерном пространстве с помощью векторов

Все сказанное об особенностях таких двумерных графиков остается справедливым и для графиков трехмерных. В частности, для обеспечения достаточной наглядности нужно тщательно отлаживать форматы представления таких графиков.

В отличие от векторных графиков, контурные графики поверхностей, наложенные на сами эти поверхности, нередко повышают восприимчивость таких поверхностей — подобно изображению линий каркаса. Для одновременного построения поверхности и контурных линий на них служит функция contourplot3d. Пример ее применения показан на рис. 8.31.

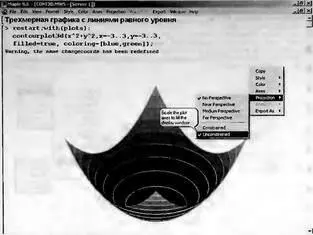
Рис. 8.31. График поверхности с контурными линиями

Для повышения наглядности этот график доработан с помощью контекстной панели инструментов графиков. В частности, включена функциональная окраска и подобраны углы обзора фигуры, при которых отчетливо видны ее впадина и пик. О возможностях переформатирования графика свидетельствует контекстное меню, показанное на рис. 8.31.

Приведенные выше достаточно простые примеры дают представление о высоком качестве визуализации геометрических фигур с помощью пакета plots. Здесь мы рассмотрим еще несколько примеров визуализации трехмерных фигур. Многие видели катушки индуктивности, у которых провод того или иного диаметра намотан на тороидальный магнитный сердечник. Некую математическую абстракцию такой катушки иллюстрирует рис. 8.32.

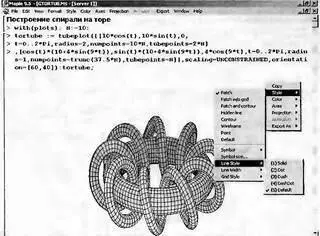
Рис. 8.32. Тор с обмоткой — толстой спиралью

В документе рис. 8.32 для функции tubeplot использовано довольно большое число параметров. Не всегда их действие очевидно. Поэтому на рис. 8.33 показано показано построение тора с тонкой обмоткой. Здесь также показано меню правой клавиши мыши, позволяющее менять стиль построения графика. Можно также поэкспериментировать с управляющими параметрами графика, от которых сильно зависят его представительность и наглядность.

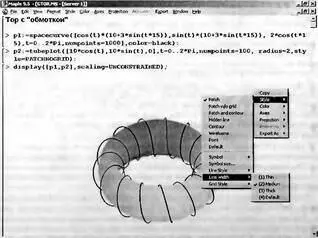
Рис. 8.33. Тор с тонкой обмоткой

В ряде случаев наглядно представленные фигуры можно строить путем объединения однотипных фигур. Пример графика подобного рода представлен на рис. 8.34. Здесь готовится список графических объектов s, смещенных по вертикали. С помощью функции display они воспроизводятся на одном графике, что повышает реалистичность изображения.

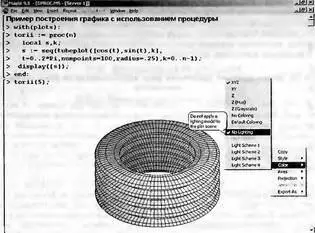
Рис. 8.34. Построение фигуры, напоминающей шину автомобиля

Последний пример имеет еще одну важную особенность — он иллюстрирует задание графической процедуры, в теле которой используются функции пакета plots. Параметр n этой процедуры задает число элементарных фигур, из которых строится полная фигура. Таким образом, высотой фигуры (или шириной «шины») можно управлять. Возможность задания практически любых графических процедур средствами Maple-языка существенно расширяет возможности Maple.

Наглядность таких графикой, как графики плотности и векторных полей может быть улучшена их совместным применением. Такой пример показан на рис. 8.35.

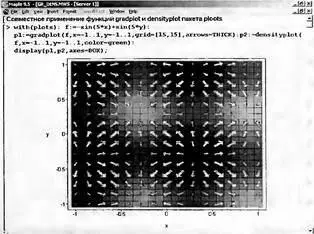
Рис. 8.35. Пример совместного применения графиков плотности и векторного поля

Этот пример иллюстрирует использование «жирных» стрелок для обозначения векторного поля. Наглядность графика повышается благодаря наложению стрелок на график плотности, который лучше, чем собственно стрелки, дает представление о плавности изменения высоты поверхности, заданной функцией f.

В пакет Plots СКМ Maple 9.5 введена новая функция для сравнения двух зависимостей f(z) и g(z) комплексного аргумента z. Функция может использоваться в нескольких формах:

plotcompare(f(z), g(z), z = a+c*I..b+d*I, options);

plotcompare(f(z) = g(z), ...);

plotcompare(f, g, a+c* I..b+d*I, options);

plotcompare(f=g, ...);

Здесь a, b, c, d - константы реального типа. Функция на одном рисунке строит графики действительной и мнимой частей зависимостей f(z) и g(z). С помощью опций можно менять цветовую гамму рисунков, их ориентацию в пространстве и др. характеристики графиков. В справке по данной функции дается множестве примеров ее применения, так что ограничимся одним, показанным на рис. 8.36.

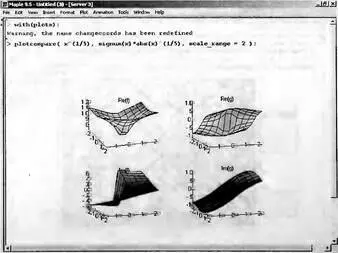
Рис. 8.16. Пример графического сопоставления двух зависимостей от комплексного аргумента

Сравнение графиков двух зависимостей, представленных на рис. 8.36 наглядно выявляет существенные отличия этих зависимостей. Достаточно отметить, что на графиках действительных частей зависимостей в одном случае видна выпуклая, а в другом случае вогнутая поверхности. Еще сильнее отличия в графиках мнимых частей сопоставляемых зависимостей.