Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Рис. 8.54. Семейство кардиоид на одном графике и крест из пяти фигур на комплексной плоскости

Вторая фигура представляет собой пять фигур, построенных функций complexplot, дающей построение графиков функций комплексной переменной на комплексной плоскости. В данном случае фигуры образуют крест.

По образу и подобию приведенных фигур читатель может опробовать свои силы в создании новых красочных фигур в полярной системе координат. Некоторые из них поразительно напоминают снежинки, картинки в калейдоскопе и изображения морских звезд. Если убрать параметр color=black, введенный ради черно-белой печати картинок в книге, то можно усилить красочность фигур за счет их разноцветной окраски.

Импликативные функции нередко имеют графики весьма любопытного вида. Ограничимся парой примеров построения таких графиков, представленных на рис. 8.55. Эти фигуры напоминают контурные графики функции двух переменных.

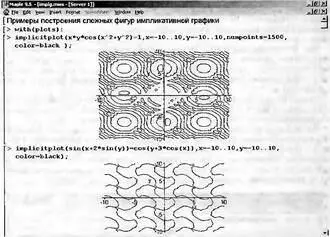
Рис. 8.55. Построение сложных фигур, изданных импликативными функциями

Приведенные примеры дают весьма наглядное представление о больших возможностях визуализации решений самых различных задач в системе Maple Можно значительно расширить их, эффектно используя описанные ранее приемы анимации изображений. В целом надо отметить, что графические возможности Maple дают новый уровень качества графики современных математических систем, о котором с десяток лет тому назад можно было только мечтать.

Maple дает прекрасные возможности для визуализации поверхностей, имеющих множество пиков и впадин, другими словами, экстремумов. Рисунок 8.56 показывает задание «вулканической» поверхности с глубокой впадиной, окруженной пятью пиками. Здесь полезно обратить внимание на способ задания такой поверхности f(a, b, с) как функции трех переменных a, b и с. Он обеспечивает индивидуальное задание координат каждого экстремума и его высоты (отрицательной для впадины).

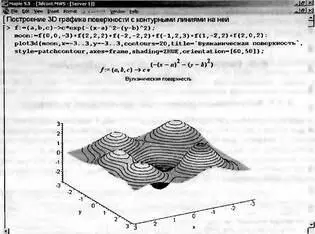
Рис. 8.56. Построение графика поверхности с множеством экстремумов

Наглядность этого графика усилена за счет применения функциональной окраски и контурных линий, нанесенных на саму поверхность. Все эти возможности обеспечивают параметры основной функции plot3d.

А на рис. 8.57 представлен еще один способ задания поверхности — с помощью функции двух угловых переменных f(θ, φ).

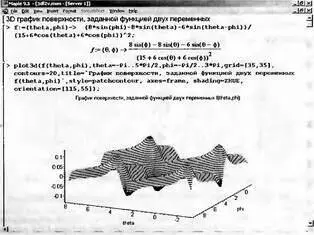
Рис. 8.57. Построение графика поверхности, заданной функцией двух угловых переменных

При построении этого рисунка также используются функциональная окраска и построение контурных линий.

Системы линейных уравнений могут решаться как с помощью функции solve, так и с помощью матричных методов. Замечательной возможностью функции solve является возможность решения относительно ограниченного числа переменных. Например, систему линейных уравнений с переменными х, у, z, t и v можно решить относительно только первых трех переменных х, у и z. При этом решения будут функциями относительно переменных t и v и можно будет построить наглядный график решения (рис. 8.58).

Рис. 8.58. График, представляющий решения системы линейных уравнений

На рис. 8.58 система задана пятью равенствами: e1, e2, e3, е4 и е5. Затем функцией solve получено вначале решение для всех переменных (для иллюстрации), а затем для трёх переменных х, у и z. Для получения решения в виде списка, а не множества, как в первом случае для всех переменных, использована функция подстановки subs. После этого функция plot3d строит плоскость решения в пространстве.

Пожалуй, еще более полезным и наглядным средством является визуализация решения системы уравнений в виде неравенств. В пакете plots имеется специальная графическая функция inequal, которая строит все граничные линии неравенств и позволяет раскрасить разделенные ими области различными цветами:

inequal(ineqs, xspec, yspec, options)

Параметры этой функции следующие: ineqs — одно или несколько неравенств или равенств или список неравенств или равенств; xspec — xvar=min_x..max_x; yspec — yvar=min_y..max_y; о — необязательные параметры, например, указывающие цвета линий, представляющих неравенства или равенства, и областей, образованных этими линиями и границами графика. Пример применения этой функции представлен на рис. 8.59.

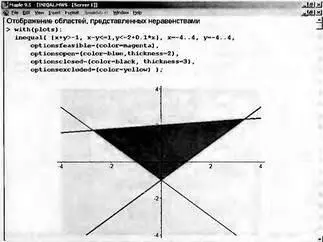
Рис. 8.59. Пример графической интерпретации решения системы неравенств

Обратите внимание на задание цветов: optionsfeasible задает цвет внутренней области, для которой удовлетворяются все неравенства (равенства), optionsopen и optionsclosed задают цвета открытых и закрытых границ областей графика, optionsexcluded используется для цвета внешних областей. График дает весьма наглядную интерпретацию действия ряда неравенств (или равенств).

Классическим методом решения нелинейных уравнений является сведение их к виду х = f(x) и применение метода простых итераций х k = s(х k-1) при заданном значении x 0. Приведем пример такого решения:

> f := х ->3*ln(x+1);

> x||0 := 0.5;

> x0 := .5;

> for k from 1 to 16 do x||k := evalf(f(x||(k-1))); od;

Нетрудно заметить, что значения х_k в ходе итераций явно сходятся к некоторому значению. Проведем проверку решения, используя встроенную функцию solve: