Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
fortran(expr,filename=str,optimized)
Два последних параметра не обязательны при выводе выражения expr в форме, присущей языку Фортран:
> fortran(а*х^2+b*х+с);
t0 = а*х**2+b*х+с
> fortran(diff(х^n,х$2));
t0 = x**n*n**2/x**2-x**n*n/x**2
Параметр optimize позволяет генерировать оптимизированные коды:
> fortran(а*х^2+b*х+с,optimized);
t1 = х**2
t4 = a*t1+b*x+c
При этом вычислительный процесс строится так, чтобы минимизировать число арифметических операций.
2.8.3. Вывод на языке С
Язык С (Си) также широко используется для решения вычислительных задач. Достаточно отметить, что сама система Maple 9.5/10 создана на языке С. Для вывода на языке С вначале надо подключить соответствующую функцию:
> with(codegen, С);
Затем можно использовать функцию С:
С(expr,folename=str,optimized)
Например:
> С(diff(х^b, х$2)) ;
t0 = pow(х,1.0*b)*b*b/(х*х)-pow(х,1.0*b)*b/(х*х);
> С(diff(х^b,х$2),optimized);
t1 = pow(x,1.0*b); t2 = b*b; t4 = x*x; t5 = 1/t4;
t9 = t1*t2*t5-t1*b*t5;
Обширные возможности преобразования выражений в различные формы представляет функция convert. А функция interface позволяет управлять выводом.
Глава 3
Работа с математическими выражениями и функциями
Центральным понятием математики являются математические выражения, которые представляют собой конструкции, созданные с помощью констант, переменных, операторов и функций. В этой главе описана практика работы с выражениями, вычисляемыми с помощью встроенных в Maple 9.5/10 операторов и функций — как элементарных, так и специальных.
3.1. Работа с операторами
3.1.1. Операторы и операнды
Операторы являются специальными знаками, которые используются в записях математических выражений для указания того, какие виды операций должны в них выполняться. Наиболее распространенными, и одинаковыми во всех системах компьютерной математики, являются арифметические операторы + (сложения), — (вычитания), * (умножения), / (деления) и возведения в степень ^. К операторам относятся круглые ( ), квадратные [ ] и фигурные {} скобки, разделительная точка, запятая, двоеточие, точка с запятой и др. Операторы применяются совместно с данными, которые они используют и которые именуются операндами.
Операнды, используемые совместно с операторами, могут быть числами, константами, переменными и математическими выражениями. К примеру, в выражении (2+3)+5 операторами являются знаки + и скобки ( ), а операндами — константы 2 и 3 для первого оператора сложения и выражение (2 + 3) и константа 5 для второго оператора сложения. Аналогично в выражении (а+b)–с операндами будут переменные a, b и с.
Следует отметить, что в математических выражениях операторы имеют общепринятый приоритет , то есть порядок выполнения операторов в сложном выражении. Низшим приоритетом обладают операторы сложения и вычитания. Более высокий приоритет у операторов умножения, деления, затем возведения в степень, выполнения логических операций и так далее. Для изменения приоритета операций в математических выражениях используются круглые скобки. Выражения в скобках выполняются в первую очередь вне зависимости от приоритета входящих в них операций. Степень вложения скобок во всех современных математических системах не ограничивается.
Понятие приоритета облегчает однозначную интерпретацию математических выражений. К примеру, в выражении 2+3*5 вначале будет вычислено 3*5, а затем к результату прибавится 2. В итоге будет вычислено значение 17. А в выражении (2+3)*5 вначале будет вычислено выражение в скобках (2+3), затем оно будет умножено на 5, так что результат будет 25. Таким образом скобки позволяют менять приоритет операций. Степень вложения скобок в современных системах компьютерной математики не ограничена. Однако иногда применение лишних скобок может повлиять на выбор правил вычисления выражений, например при вычислении степеней.
3.1.2. Виды операторов
Формально операторы представлены своими идентификаторами в виде специальных математических знаков, слов и иных имен. Операторы, как это вытекает из их названия, обеспечивают определенные операции над данными, представленными операндами. Имеется пять основных типов операторов:
• binary — бинарные операторы (двумя операндами);
• unary — унарные операторы (с одним операндом);
• nullary — нуль-арные операторы (без операнда — это одна, две и три пары кавычек);
• precedence — операторы старшинства (включая логические операторы);
• functional — функциональные операторы.
Для просмотра операторов и их свойств можно использовать следующие команды вида:
> ?operators[вид];
где вид — название вида оператора, указанное выше. Будет выведена страница справки по операторам заданного вида. А для изучения примеров применения операторов нужно задать и исполнить команду
> ?operators[examples];
Команда
> ?define;
позволяет ознакомиться с функций define. С ее помощью можно определять новые операторы.
3.1.3. Применение бинарных (инфиксных) операторов
Бинарные операторы , именуемые также инфиксными , используются с двумя операндами, обычно размещаемыми по обе стороны от оператора. В ядро Maple включено около трех десятков бинарных операторов. Основные из них перечислены в таблице 3.1. Чуть позже мы рассмотрим и другие бинарные операторы. Примеры вычисления выражений с бинарными операторами (файл ор):
> 2+3-(-4);
> [2^3,2**3];
> 7 mod 5;
> [3@2,3@@2];
> [х@х,х@@х];
> [х$3,х$4];
Таблица 3.1. Бинарные операторы
| Обозначение | Оператор | Обозначение | Оператор |
|---|---|---|---|
| + | Сложение | @ | Оператор композиции |
| - | Вычитание | @@ | Повторение композиции |
| * | Умножение | , | Разделитель выражений |
| / | Деление | := | Присваивание |
| ** или ^ | Возведение в степень | .. | Задание интервала |
| mod | Остаток от деления | , | Разделитель выражений |
| $ | Оператор последовательности | &* | Некоммутативное умножение |
| . | Разделительная точка | & | Нейтральный оператор |
| || | Конкатенация (объединение) |
> int(х^2,х=1..4);
> S: = `Hello` || ` my ` || `friend!`;
Оператор композиции @@ может использоваться для создания и вычисления сложных функций, содержащих цепные дроби:
> f:=а->1/(1+а);(f@@3)(а);
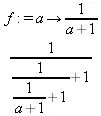
> f(5);
Интервал:
Закладка:










