Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Для проверки предполагаемого имени на уникальность достаточно выполнить команду ?name, где name — выбранное имя. Если при этом откроется окно справки с этим именем, значит, оно уже использовано в Maple. Лучше воздержаться от его применения, так как связанная с этим именем команда или функция перестает работать, как только это имя закрепляется за какой-либо переменной.

Поскольку Maple 9.5 прежде всего система символьной математики, то по умолчанию любые переменные рассматриваются как объекты символьного типа. Благодаря этому такие переменные могут фигурировать в математических выражениях, (таких как sin(x)/x), без их предварительного объявления. В отличие от обычных языков программирования такое использование переменных не влечет за собой появления сообщений об ошибках и является более естественным.

Для присваивания переменным конкретных значений используется комбинированный символ присваивания «:=», например:

n:=1 — переменной n присваивается целочисленное значение 1;

х:=123.456 — переменной х присваивается вещественное значение 123.456;

у:=17/19 — переменной у присваивается рациональное значение 17/18;

name:=`Piter` — переменной name присваивается строковое значение `Piter`;

expr:=2*Pi/3 — переменной expr присваивается значение выражения 2л??!!/3;

V:=[1,2,3] — переменной V присваивается значение списка чисел [1,2,3];

М:=[[1,2,3],[4,5,6]] — переменной М присваивается значение двумерного массива;

f:=x->x^2 — переменной f присваивается значение функции пользователя f(x)=x^2.

Правая часть выражения присваивания определяет тип переменной. Например, она может быть целочисленной, действительной, строковой, индексированной (элемент массива) и т.д.

Переменная, имеющая какое либо значение, занимает в памяти намного больше места, чем неопределенная переменная. У последней место в памяти занимают только символы идентификатора. Поэтому нередко целесообразно отменить присваивание у тех переменных, которые в дальнейшем можно не использовать. Это может понадобиться и в том случае, когда какую-либо переменную с численным или иным значением нужно использовать просто как неопределенную переменную. Рассмотрим следующий пример:

> х:=10;

> х;

> int(х^2,x);

Error, (in int) wrong number (or type) of arguments

Здесь не удалось вычислить интеграл с подынтегральной функцией х^2 из-за того, что переменная х уже определена ранее как целочисленная переменная со значением 10, тогда как для вычисления интеграла она должна быть необъявленной или строковой (убедитесь в этом сами).

Для отмены присваивания надо использовать следующее выражение:

> х: =`х`;

Итак, заключение имени переменной в прямые апострофы ликвидирует присваивание. Так что запись х:=`х` означает, что переменной х возвращается статус неопределенной переменной. Теперь можно вычислить интеграл:

> int(х^2,х);

Можно сделать переменную х неопределенной и с помощью выражения вида x:=evaln(x). Это поясняет следующий пример:

> х:=123;

> x:=evaln(x);

> int(х^n,х);

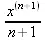
Для отмены присваивания значений разом всем переменным (и введенным функциям пользователя) можно использовать команду restart. Следующий пример поясняет ее применение:

> х:=5;

> х^2;

> restart;

> х;

> х^2;

Следует отметить, что команда restart отменяет все предшествующие определения, что иногда чревато осложнениями. Применяйте ее только тогда, когда вы уверены, что предшествующая заданной часть документа (или даже ряда документов) действительно не важна.

Важно отметить, что Maple сохраняет в памяти все определения и присваивания, которые были сделаны во всех загруженных в систему документах. Поэтому результаты вычислений в текущем документе могут зависеть от определений в других документах. Команда restart позволяет исключить эту зависимость.

В большинстве расчетов пользователей Maple вполне удовлетворяет статус переменных, соответствующий присвоенным им значениям. Однако серьезные расчеты предполагают, что переменные могут иметь определенные ограничения — например, они не должны принимать отрицательных значений при обычном вычислении квадратного корня или логарифма числа.

Для придания переменным статуса предполагаемых используется функция assume:

assume(x,prop)

где х — переменная, имя или выражение, prop — свойство. Следующие примеры (файл assume) показывают применение функции assume:

> restart;

> assume(х,positive);

> х;

> s:=x->sqrt(х);

> s(2);

> s(2.);

> s(-2);

> is(x,positive);

> is(x,negative);

>> about(x);

Originally x, renamed x~: is assumed to be: RealRange(Open(0), infinity)

Обратите внимание, что в этом примере переменная х помечена как положительная и при выводе сопровождается знаком тильды ~, как бы предупреждающем нас о ее особом статусе. Это не означает, что она не может принять отрицательное значение. Однако с помощью функции is можно убедиться в ее особом статусе и при необходимости программным путем исключить вычисления для х<0. Кроме того, о свойствах переменной можно узнать с помощью функции about(name).

Иногда к уже имеющимся признакам надо добавить новые. Для этого используется функция additionally:

> assume(a,nonnegative);

> additionally(а<=0);

> about(а);

Originally a, renamed а~: is assumed to be: 0

В этом примере переменной а вначале задан признак положительности, а затем а<=0. Оба признака удовлетворяются только при a=0, что и подтверждает вывод информации о статусе этой переменной функцией about(a).

Предполагаемую переменную можно также изменить путем присваивания ей нового значения, противоречащего ее статусу:

> а:=123;

> about(а);

123:

All numeric values are properties as well as objects. Their location in the property lattice is obvious, in this case integer.

Для отмены переменным статуса предполагаемых используются те же приемы, что и при отмене присвоенного значения. Например, запись х:='х' отменяет статус предполагаемой для переменной х.

К числу широко распространенных данных относятся файловые данные , которые представлены файлами. Файлом называют имеющую имя упорядоченную совокупность данных, размещенную на том или ином носителе — обычно на жестком, гибком или компакт-диске.