Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

При обычной арифметике был бы получен 0 или сообщение о некорректности операций из за превышения разрядной сетки компьютера.

А вот еще более характерный пример такого рода. Пусть вероятность рождения мальчика 0.515. Какова вероятность того, что среди 1000 новорожденных мальчиков будет не менее половины. Расчетная формула требует вычисления факториала 1000!:

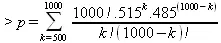
> evalf(%);

Если увеличить число рождаемых мальчиков до 10 или 100 тысяч, то такая задача может послужить хорошим тестом не только на работу с очень большими числами, но и на скорость вычислений. Решение таких задач без применения аппарата точной арифметики больших чисел встречает большие трудности, а подчас и просто невозможна.

Несколько хорошо известных функций использует при вычислениях средства сравнения чисел. Для действительного аргумента х это следующие функции:

• trunc(x) — при х>=0 возвращает наибольшее целое, меньшее или равное х, при x<0, trunc(x) = -trunc(-x).

• round(x) — округляет x до ближайшего целого.

• frac(x) — возвращает дробную часть х, так что frac(x) = х - trunc(x).

• floor(x) — возвращает наибольшее целое, меньшее или равное х.

• ceil(x) — возвращает наименьшее целое, большее или равное х.

Эти функции могут использоваться и для комплексного аргумента х. При этом справедливы следующие соотношения:

trunc(x) = trunc(Re(x)) + I*trunc(Im(x))

round(x) = round(Re(x)) + I*round(Im(x))

frac(x) = frac(Re(x)) + I*frac(Im(x))

ceil(x) = -floor(-x)

К этой категории относится и функция знака, синтаксис которой:

signum(x) signum(1,x) signum(0, х, у)

В основной (первой) форме она возвращает значение x/abs(x), где функция abs(x) — возвращает абсолютное значение действительного х, т.е. х при х> 0 и -х при х<0.

Действия, выполняемые этими функциями, вполне очевидны и читатель может легко проверить это на практике. Данные функции можно использовать для моделирования периодически повторяющихся зависимостей (сигналов). Несколько таких примеров представлено ниже (файл modsig — рис. 3.1):

> restart;

RC:=2-2*ехр(3*(floor(t/2)-t/2));

upside:=1/(3+2*sin(Pi*t));

sawtooth:=t-floor(t):

roundsquare: = (tanh(100*sin(Pi*t) )+1) /2:

squarewave:= (1+signum(sin (Pi*t)))/2;

blimps:=squarewave*sawtooth;

triang:=blimps+(squarewave-1)*(sawtooth-1);

plot([sawtooth+5, upside+3, RC,blimps-2,squarewave-4,roundsquare-6,triang-8],t=0..10,-8..6,

color=[red,orange,green,black,magenta,brown,blue], thickness=3);

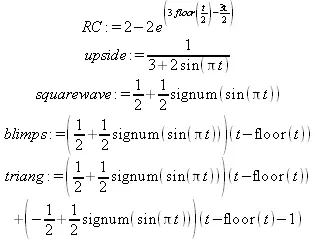
Графики зависимостей, получаемые с помощью представленного выше примера показаны на рис. 3.1. Эти зависимости можно использовать в качестве моделей сигналов при моделировании электрических и электронных цепей (см. главу 11).

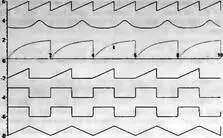
Рис. 3.1. Графики зависимостей, получаемых с помощью функций сравнения

В ядре Maple (и других СКМ) определены следующие тригонометрические функции : sin — синус; cos — косинус; tan — тангенс; sec — секанс; csc — косеканс; cot — котангенс. Все эти функции являются периодическими (с периодом 2π, кроме тангенса и котангенса, у которых период равен π) и определены для действительного и комплексного аргументов. Примеры вычислений (файл calcfun):

> [sin(1), sin(1.)];

> sin(x)^2+cos(x)^2;

> simplify(%);

> simplify(tan(x)*cos(x));

> sec(2+3*1);

> sec(2.+3*I);

> cot(I);

> csc(I);

Многие свойства тригонометрических функций можно оценить, рассматривая их графики. Для построения таких графиков средствами Maple можно использовать функцию plot. Примеры построения графиков тригонометрических функций даны в файле tfris.

Фундаментальная роль функций синуса и косинуса проявляется в решении задач спектрального анализа и синтеза. В Maple они реализуются с помощью функций прямого и обратного преобразований Фурье [39, 43]. Однако, смысл гармонического синтеза проще всего понять, просто суммируя синусоидальные функции с кратной частотой — гармоники. При этом характер результирующего колебания зависит от того, какие гармоники берутся (все, только четные или только нечетные), а также от того, по какому закону меняется амплитуда колебаний и их фаза в зависимости от номера гармоники. Покажем это на паре примеров.

На рис. 3.2 показан пример гармонического синтеза двух периодов пилообразного колебания (сигнала) при суммировании 3, 10 и 60 гармоник. Отчетливо видно, что по мере увеличения числа гармоник форма колебаний действительно приближается к треугольной. В условиях резкого ограничения числа гармоник в местах предполагаемого разрыва колебаний наблюдаются характерные колебания — эффект Гиббса.

Рис. 3.2. Гармонический синтез треугольных колебаний по 3, 10 и 60 гармоникам

Колебания описанной формы получаются за счет синтеза всех гармоник, причем амплитуда гармоник равна 1/k, где k — номер гармоники.

А теперь рассмотрим синтез симметричных прямоугольных колебаний, получивших название — меандр. Для синтеза меандра надо использовать только нечетные гармоники, т. е. с номерами n=1, 3, 5, … Проще всего получить нечетные числа, используя вместо параметра n значение 2n–1. Тогда для получения 3, 9 и 59 нечетных гармоник надо будет использовать значения n до 2, 5 и 30. Рис. 3.3 иллюстрирует синтез меандра.

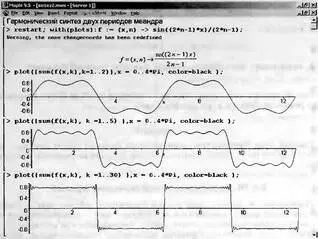
Рис. 3.3. Гармонический синтез меандра при n = 2, 5 и 30

Читатель, интересующийся вопросами гармонического синтеза сигналов может опробовать в нем свои силы и синтезировать колебания и сигналы других форм. Поскольку при синтезе сигнал получается в виде частотных составляющих (гармоник), то для преобразования такого сигнала можно использовать частотные фильтры.

К обратным тригонометрическим функциям относятся: arcsin — арксинус; arccos — арккосинус; arctan — арктангенс; arcsec — арксеканс; arccsc — арккосеканс; arccot — арккотангенс. Примеры вычислений (файл calcfun):