Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
> arcsin(.2);
> arcsin(2.);
> evalc(arcsin(5));
> arccos(1/2);
> arctan(1);
> arccot(0);
К этому классу функций принадлежит еще одна полезная функция:
arctan(y,x) = argument(х+I*у)
Она возвращает угол радиус-вектора в интервале от -Pi до Pi при координатах конца радиус-вектора х и у (см. пример ниже):
> arctan(2., 3);
Графики ряда обратных тригонометрических функций строит документ, имеющийся в файле tfris. Следует отметить, что эти функции не являются периодическими.
3.2.10. Применение гиперболических функций
Гиперболические функции представлены следующим набором: sinh — гиперболический синус; cosh — гиперболический косинус; tanh — гиперболический тангенс; sech — гиперболический секанс; csch — гиперболический косеканс; coth — гиперболический котангенс. Примеры применения гиперболических функций представлены ниже (файл calcfun):
> [sinh(1.), cosh(1.), tanh(1.)];
> [sech(1.), csch(1.), coth(1.)];
На рис. 3.4 сверху представлены графики гиперболического синуса, косинуса и тангенса. По ним можно судить о поведении этих функций.
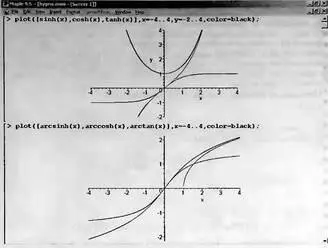
Рис. 3.4. Графики основных гиперболических и обратных гиперболических функций
В отличие от тригонометрических функций, гиперболические функции не являются периодическими. Функция гиперболического тангенса имеет симметричную кривую с характерными ограничениями. Поэтому она широко используется для моделирования передаточных характеристик нелинейных систем с ограничением выходного параметра при больших значениях входного параметра.
С помощью функции преобразования convert(f, ехр) можно перевести гиперболические функции в экспоненциальную форму:
> convert(sinh(х),ехр);
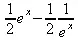
> convert(tan(х),ехр);
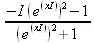
3.2.11. Обратные гиперболические функции и их применение
К обратным гиперболическим функциям относятся: arcsinh — гиперболический арксинус; arccosh — гиперболический арккосинус; arctanh — гиперболический арктангенс; arcsech — гиперболический арксеканс: arccsch — гиперболический арккосеканс: arccoth — гиперболический арккотангенс. Примеры применения:
> [arcsinh(1.),arccosh(1.), arctanh(1.)];
Графики обратных гиперболических синуса, косинуса и тангенса представлены на рис. 3.4 снизу. С помощью функции преобразования convert(f, ln) можно перевести гиперболические функции в логарифмическую форму:
> сonvert(arcsin(х), ln);
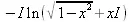
> convert(arctan(х), ln);
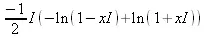
3.2.12. Вычисление степенных и логарифмических функций
К степенным и логарифмическим относятся следующие функции системы Maple: ехр — экспоненциальная функция; ilog10 — целочисленный логарифм по основанию 10 (возвращает целую часть от логарифма по основанию 10); ilog — целочисленный логарифм (библиотечная функция, возвращающая целую часть от натурального логарифма); ln — натуральный логарифм; log — логарифм по заданному основанию (библиотечная функция); log10 — логарифм по основанию 10; sqrt — квадратный корень.
Примеры вычисления этих функций (файл calcfim):
> х:=2;
> [ехр(х),ln(х),log(х),log10(х)];
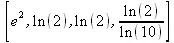
> х:=2.0;
> [ехр(х),ln(х),log(х),log10(х)];
> ilog[2](100);
> readlib(log10);
> log10(10000.);
> evalc(sqrt(2+3*I));
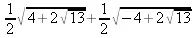
> sqrt(99+1);
Графики ряда описанных выше функций показаны на рис. 3.5. Они также получены с применением средств Maple 9.5.
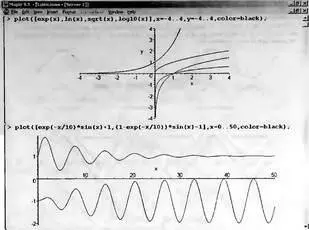
Рис. 3.5. Графики ряда степенных и логарифмических функций
На рис. 3.5 показаны также графики синусоиды с экспоненциально падающей и нарастающей амплитудой. Строго говоря, называть представленные функции синусоидами математически не корректно.
Многие функции этой группы обычно определены для положительных значений аргумента. Однако введение комплексных чисел позволяет вычислять такие функции и для отрицательных значений аргумента. Несколько интересных примеров этого представлено ниже (файл calcfun):
> restart:sqrt(-4);
> simplify( sqrt(х^2));
> ln( -1 );
> simplify(log(exp(x)));
> assume(x,positive);simplify(log(exp(x)));
Обратите внимание на то, что в предпоследнем примере Maple отказалась вычислить «очевидное» значение выражения, но сделала это после придания х статуса предполагаемой переменной с только положительными значения.
3.2.13. Применение элементарных функция для моделирования сигналов
Системы компьютерной математики часто используются для моделирования сигналов и устройств их обработки и преобразования (см. пример в разделе 3.2.5). Рисунок 3.6 показывает построение нескольких функций, полученных с помощью комбинаций элементарных функций, включая тригонометрические функции. Такие комбинации позволяют получать периодические функции, моделирующие сигналы стандартного вида: в виде напряжения на выходе двухполупериодного выпрямителя, симметричных прямоугольных колебаний (меандр), пилообразных и треугольных импульсов, треугольных импульсов со скругленной вершиной.
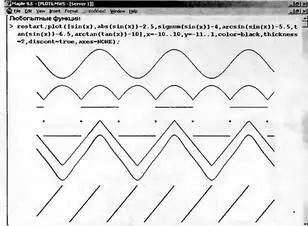
Рис. 3.6. Примеры моделирования сигналов с помощью комбинаций элементарных функций
В этом рисунке запись axes=NONE убирает координатные оси. Обратите внимание, что смещение графиков отдельных функций вниз с целью устранения их наложения достигнуто просто прибавлением к значению каждой функции некоторой константы.
Приведенные выше сигналы нередко можно формировать, используя функции с условиями — например, функцию signum. Однако достоинство моделирования сигналов с помощью только элементарных функций заключается в том, что такие сигналы нередко могут обрабатываться аналитически, тогда как для функций с условиями это возможно далеко не всегда.
Читать дальшеИнтервал:
Закладка:










