Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Интегральная показательная функция определяется следующим образом:
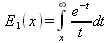
Гамма-функция определяется выражением:
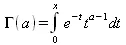
Неполная гамма-функция определяется как:
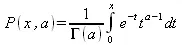
Перейдем к функциям, представляющим ортогональные полиномы. Функция Лежандра определяется следующим образом:
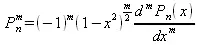
где Р n (х) — полином Лежандра степени n, определяется так:
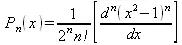
3.3.2. Специальные математические функции системы Maple 9.5
Maple 9.5 имеет практически полный набор специальных математических функций:
• AiryAi (Bi) — функции Эйри;
• AngerJ — функция Ангера;
• bernoulli — числа и полиномы Бернулли;
• Bessell (J, K, Y) — функции Бесселя разного рода;
• Beta — бета-функция;
• binomial — биноминальные коэффициенты;
• Chi — интегральный гиперболический косинус;
• Сi — интегральный косинус;
• csgn — комплексная сигнум-функция;
• dilog — дилогарифм;
• Dirac — дельта-функция Дирака;
• Ei — экспоненциальный интеграл;
• EllipticCE (CK, CPi, Е, F, K, Modulus, Nome, Pi) — эллиптические интегралы;
• erf — функция ошибок;
• erfc — дополнительная функция ошибок;
• euler — числа и полиномы Эйлера;
• FresneIC (f, g, S) — интегралы Френеля;
• GAMMA — гамма-функция;
• GaussAGM — арифметико-геометрическое среднее Гаусса;
• HankelH1 (Н2) — функции Ганкеля;
• harmonic — частичная сумма серии гармоник;
• Heaviside — функция Хевисайда;
• JacobiAM (CN, CD, CS, DN, DC, DS, NC, ND, NS, SC, SD, SN) — эллиптические функции Якоби;
• JacobiTheta1 (2, 3, 4) — дзета-функции Якоби;
• JacobiZeta — зет-функция Якоби;
• KelvinBer (Bei, Her, Hei, Ker, Kei) — функции Кельвина;
• Li — логарифмический интеграл;
• InGAMMA — логарифмическая гамма-функция;
• MeijerG — G-функция Мейджера;
• pochhammer — символ Похгамера;
• polylog — полилогарифмическая функция;
• Psi — дигамма-функция;
• Shi — интегральный гиперболический синус;
• Si — интегральный синус;
• Ssi — синусный интеграл смещения;
• StruveH (L) — функции Струве;
• surd — неглавная корневая функция;
• LambertW — W-функция Ламберта;
• WeberE — Е-функция Вебера;
• WeierstrassP — Р-функция Вейерштрасса;
• WeierstrassPPrime — производная Р-функции Вейерштрасса;
• WeierstrassZeta — зета-функция Вейерштрасса;
• WeierstrassSigma — сигма-функция Вейерштрасса;
• Zeta — зета-функция Римана и Гурвица.
Ввиду большого числа специальных функций и наличия множества примеров их вычисления в справочной системе Maple 9.5, ограничимся несколькими примерами вычисления наиболее распространенных специальных функций. По их подобию читатель может опробовать в работе и другие специальные функции.
На рис. 3.13 даны примеры применения ряда специальных функций. Обратите особое внимание на первый пример. Он показывает, как средствами системы Maple задается определение функций Бесселя. Показано, что функции Бесселя являются решениями заданного на рис. 3.13 дифференциального уравнения второго порядка. Система Maple 9.5/10 способна вычислять производные и интегралы от специальных функций.
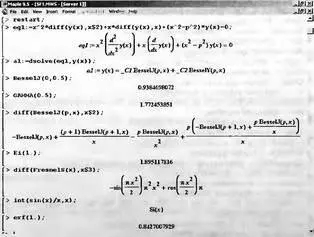
Рис. 3.13. Примеры применения специальных функций
Еще несколько примеров работы со специальными функциями представлено на рис. 3.14. Как видно из приведенных примеров, на экране монитора можно получить математически ориентированное представление специальных функций, обычно более предпочтительное, чем представление на Maple-языке или в текстовом формате. Записи функций при этом выглядят как в обычной математической литературе.

Рис. 3.14. Примеры работы со специальными математическими функциями
На рис. 3.14 показаны примеры разложения специальных функций в ряды и применения функции convert для их преобразования. Любопытно отметить, что в двух первых примерах рис. 3.14 вывод оказался иным, чем в предшествующих версиях Maple. Да и в них вывод для этих примеров отличался. Это говорит о непрерывной работе разработчиков над алгоритмами символьных вычислений и необходимости переработки примеров при переходе от одной версии Maple к другой.
3.3.3. Построение графиков специальных функций
Много информации о поведении специальных функций дает построение их графиков. На рис. 3.15 показано построение семейства графиков функций Бесселя BesselJ разного порядка и гамма-функции. Эти функции относятся к числу наиболее известных. Если читателя интересуют те или иные специальные функции, следует прежде всего построить и изучить их графики.
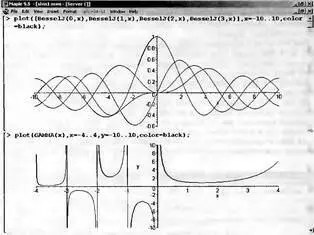
Рис. 3.15. Графики функций Бесселя и гамма-функции
3.3.4. Консультант по функциям
Математикам, серьезно работающим с функциями, большую помощь может оказать имеющийся в составе Maple 9.5 консультант по функциям, вводимый командой:
FunctionAdvisor()
FunctionAdvisor(topics, quiet)
FunctionAdvisor(Topic, function, quiet)
Здесь: topics — строковый параметр, задающий вывод тематической информации, quiet — строковый параметр, указывающий на вывод вычислительных данных, Topic — задание темы и function — задание имени функции или класса функций.
Команда FunctionAdvisor() выводит правила применения консультанта по функциям (файл funcadv):
> FunctionAdvisor(); The usage is as follows:
> FunctionAdvisor( topic, function, ... );
where 'topic' indicates the subject on which advice is required, 'function' is the name of a Maple function, and '...' represents possible additional input depending on the 'topic' chosen. To list the possible topics:
> FunctionAdvisor( topics ); A short form usage,
> FunctionAdvisor(function);
with just the name of the function is also available and displays a summary of information about the function.
Следующие примеры показывают вывод определений функций Бесселя:
> FunctionAdvisor(describe, Bessel);
BesselI = Modified Bessel function of the first kind,
BesselJ = Bessel function of the first kind,
BesselK = Modified Bessel function of the second kind,
BesselY = Bessel function of the second kind
> FunctionAdvisor(describe, BesselJ);
BesselJ = Bessel function of the first kind
В следующем примере выводится информация о представлении функции синуса в виде ряда, представленного суммой его членов:
Читать дальшеИнтервал:
Закладка:










