Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> FunctionAdvisor(sum_form, sin);

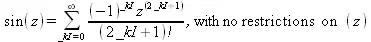
Еще один пример показывает вывод интегрального представления синусного интеграла Френеля:

> FunctionAdvisor(integral form, FresnelS);

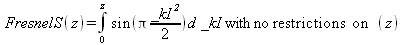
Представленные примеры дают представление лишь о малой части возможностей консультанта по функциям. С этим мощным средством получения информации о функциях можно дополнительно познакомиться по справке о нем, содержащей множество интересных примеров применения консультанта по функциям.

Функции комбинаторики достаточно известны из обычного курса математики. Но они применяются сравнительно редко. Поэтому они не включены в состав ядра системы, но имеются в пакете расширения combinat. При вызове пакета

> with(combinat);

выводится список имен его функций. Ввиду важности функций комбинаторики для некоторых специальных вычислений приведем их полные определения:

• Chi(x) — гиперболический косинусный интеграл;

• bell(n) — возвращает числа из решения уравнения ехр(ехр(х)-1)= sum(bell(n)/n!*x^n, n=0..infinity), причем для вычислений используется рекуррентное соотношение bell(n+1) = (bell(n)+1)^n;

• binomial(n, r) — возвращает биноминальные коэффициенты, причем, если n и r — целые числа, удовлетворяющие условию 0<=r<=n, то функция возвращает C(n,r)=n!/(r!(n-r)!), а в общем случае C(n, r) = limit(GAMMA(N+1)/ GAMMA(R+1)/GAMMA(N-R+1),R=r,N=n).

• composition(n, k) — возвращает списки композиций для целых неотрицательных n и k;

• fibonacci(n) — возвращает числа Фибоначчи, вычисляемые по рекуррентной формуле F(n) = F(n–1)+F(n –2), где F(0) = 0 и F(1)=1;

• fibonacci(n, х) —возвращает значение полинома Фибоначчи F ( n, х ) = х F ( n– 1, х ) + F ( n –2, х ), где F (0, х )–0 и F (1, а )=1, при этом F ( n ) =F ( n, 1);

• firstpart(n) — возвращает первый член последовательности из наборов чисел, сумма которых равна n (в оригинале каноническую последовательность);

• nextpart(1) — возвращает следующую часть указанной выше последовательности;

• lastpart(n) — возвращает последний член последовательности, указанной для функции firstpart;

• prevpart(1) — возвращает предпоследнюю часть канонической последовательности ряда;

• conjpart(1) — возвращает объединенный раздел в канонической последовательности ряда;

• graycode(n) — возвращает список кодов Грея для n-битовых чисел;

• multinomial(n, k1, k2,…, km) — возвращает мультиномиальные коэффициенты;

• numbcomb(n) и numbcomb(n, m) — возвращает число комбинаций;

• numbcomp(n, k) — возвращает число различных упорядоченных наборов из к натуральных чисел, сумма которых равна n;

• numbpart(n) — возвращает список всех возможных сумм, дающих n;

• permute(n) и permute(n, r) — возвращает numbperm(n, r) = nops(permute(n, r));

• powerset(s) — возвращает степень множества в множестве s;

• randcomb(n, m) — возвращает случайную комбинацию;

• randpart(n) — возвращает случайную часть:

• randperm(n) — возвращает случайную композицию;

• stirling1(n, m) — возвращает число Стирлинга первого рода;

• stirling2(n, m) — возвращает число Стирлинга второго рода;

• subsets(L) — задает итерационную процедуру над степенями множества или списка L;

• vectoint(I) — возвращает индекс вектора канонического упорядочения I;

• inttovec(m, n) — возвращает вектор канонического упорядочения для неотрицательных целых чисел m и n.

Следующие примеры (файл combinat) иллюстрируют применение функций комбинаторики:

> choose(4,3);

> choose([a,a,b,с],3);

> composition(3,2);

> decodepart(4,2);

> fibonacci(10);

> seq(fibonacci(i),i=1..12);

> partition(5);

> firstpart(3);

> nextpart(%);

> prevpart(%);

> lastpart(3);

> conjpart(%);

> multinomial(8,2,3,3);

> numbcomp(8,5);

> numpart(3);

> numbperm(4);

> numbperm([a, b]);

> numbperm({a,b,c}, 2);

> permute(3,2);

> permute([a,a,b],2);

> powerset([a,a,b]);

> randcomb([a,b,c,d],3);

> randcomb([a, b, c, d], 3);

> randpart(10);

> randpart(10);

> stirling1(10,5);

> stirling2(10, 5);

> S:=subsets({1,2}):

> while not S[finished] do S[nextvalue]() od;

> vectoint([1,0,0]);

> inttovec(6,3);

Еще девять функций, относящихся к структурам комбинаторики , содержит пакет combstruct:

> with(combstruct);

Эти функции служат для создания случайно однородных объектов, принадлежащих заданному комбинаторному классу. Ограничимся приведением примеров применения этих функций (файл combictruct):

> allstructs(Subset({one,two)));

> allstructs(Permutation([x,y,z]),size=2);

> count(Subset({1,2,3}));

> draw(Combination(5),size=4);

> count(Permutation([a,a,b]));

> it :=iterstructs(Permutation([a,a,b]),size=2);

> draw(Partition(9));

> allstructs(Composition(3), size=2);

В обширном пакете numtheory собран ряд функций, относящихся к теории чисел. Их можно просмотреть, используя команду:

> with(numtheory);

Большинство функций этого пакета достаточно просты и заинтересовавшийся читатель вполне в состоянии провести их тестирование самостоятельно.

Этот весьма специфический пакет содержит следующие функции для работы с р-адическими числами. Команда

> with(padic);

Выводит список имен этого пакета. Ввиду специфичности данных функций их изучение мы оставляем за читателем для самостоятельной работы — если она требует применения таких чисел.