Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> А: = [[1,2],[3,4]];

> eval(А);

> evalf(sin(1));

> evalf(sin(2)^2+cos(2)^2,20);

> evalhf(sin(1));

> evalm(20*A+1);

> 1<3;

> evalb(1<3);

> readlib(shake) : evalr(min(2,sqrt(3) )) ;

> evalr(abs(x));

> shake(Pi,3);

В дальнейшем мы многократно будем применять функции оценивания для демонстрации тех или иных вычислений.

Maple может работать не только с одиночными выражениями, но и с последовательностями выражений. Последовательность выражений — это ряд выражений, разделенных запятыми и завершенный фиксатором (файл expr1):

> a, y+z, 12.3, cos(1.0);

Для автоматического формирования последовательности выражений применим специальный оператор $, после которого можно указать число выражений или задать диапазон формирования выражений:

> f$5;

> $1..5;

> (n^2)$5;

> (n^2)$n=0..5;

> Vl[i]$i=1..5;

Для создания последовательностей выражений можно использовать также функцию seq:

> seq(sin(х),х=0..5);

> seq(sin(x*1.),x=0..5);

> seq(f1(1.),f1=[sin,cos,tan]);

> sin(1.0), cos(1.0), tan(1.0);

При выполнении порой даже простых операций результаты получаются чрезвычайно громоздкими. Для повышения наглядности выражений Maple выводит их с выделением общих частей выражений и с присваиванием им соответствующих меток. Метки представлены символами %N, где N — номер метки.

Помимо меток при выводе результатов вычислений могут появляться и другие специальные объекты вывода, например корни RootOf, члены вида O(x^n), учитывающие погрешность при разложении функций в ряд, и обозначения различных специальных функций, таких как интегральный синус, гамма-функция и др. Примеры такого вывода приведены ниже:

> solve(х^7-х^2-1,х);

> taylor(sin(x),x,5);

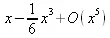
Часто встречаются также знаки ~ для отметки предполагаемых переменных, постоянные интегрирования и другие специальные обозначения. По мере упоминания в тексте таких объектов вывода они будут описаны.

Выражения (expr) или уравнения (eqn) обычно используются как сами по себе, так и в виде равенств или неравенств. В последнем случае объекты с выражениями имеют левую и правую части. Для простейших манипуляций с выражениями полезны следующие функции:

• cost(a) — возвращает число сложений и умножений в выражении а (функция пакета codegen);

• lhs(eqn) — выделяет левую часть eqn;

• rhs(eqn) — выделяет правую часть eqn;

• normal(expr) — дает нормализацию (сокращение) expr в виде дроби;

• numer(expr) — выделяет числитель expr;

• denom(expr) — выделяет знаменатель expr.

Ввиду очевидности действия этих функций ограничимся наглядными примерами их применения:

> with(codegen,cost):

> cost(х^3+b^2-х);

> lhs(sin(x)^2+cos(x)^2=1);

> rhs(sin(x)^2+cos(x)^2=1);

> normal(2/4+3/6+6/12);

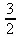
> f:=5*(a-b)^2/(а^2-2*а*b-b^2);

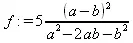
> numer(f);

> denom(f);

Обратите внимание на то, что в старых версиях (до Maple 7) загрузка библиотечной функции cost выполнялась иначе — командой readlib(cost). Это обстоятельство может служить причиной неверной работы документов, созданных в старых версиях Maple, в среде последующих версий Maple.

В общем случае выражения могут быть многоуровневыми и содержать объекты, расположенные на разных уровнях вложенности. Приведем две функции для оценки уровней выражений и списков:

• nops(expr) — возвращает число объектов первого уровня (операндов) в выражении expr;

• op(expr) — возвращает список объектов первого уровня в выражении expr;

• op(n,expr) — возвращает n-й объект первого уровня в выражении expr. Ниже представлены примеры применения этих функций:

> nops(а+b/с);

> op(a+b/c);

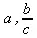
> op(1,a+b/c);

> op(2,a+b/c);

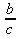
Рекомендуется просмотреть и более сложные примеры на применение этих функций в справке.

Многие математические выражения имеют различные тождественные формы. Порою преобразование выражения из одной формы в другую позволяет получить результат, более удобный для последующих вычислений. Кроме того, различные функции Maple работают с разными формами выражений и разными типами данных. Поэтому большое значение имеет целенаправленное преобразование выражений и данных.

Основной функцией для такого преобразования является функция

convert: convert(expr, form, arg3,...)

Здесь expr — любое выражение, form — наименование формы, arg3, … — необязательные дополнительные аргументы.

convert — простая и вместе с тем очень мощная функция. Ее мощь заключается в возможности задания множества параметров. Их полный перечень (около восьмидесяти наименований) можно найти в справке по функции convert. Многие из этих параметров очевидны с первого взгляда, поскольку повторяют наименования типов чисел, данных или функций. Например, опции binary, decimal, hex и octal преобразуют заданные числа в их двоичное, десятичное, шестнадцатиричное и восьмеричное представление. Параметр vector задает преобразование списка в вектор (напоминаем, что список и вектор — разные типы данных), а параметр matrix — в матрицу. Приведем примеры применения функции convert (файл expr1):

> convert(123,binary);