Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Еще одна иногда полезная функция контроля выражений depends(f,x) возвращает true, если х входит в f и false в противном случае. При этом надо также помнить, что функция (выражение) оценивается и исполняется. Следующие примеры хорошо иллюстрируют сказанное:
> depends(2+2*sin(x),х);
> depends(int(х^2,х),х);
> depends(int(х^2,х=0..1), х)
В последнем примере вычисленное выражение это уже просто число, в нем х не содержится, а потому и получено значение false.
3.6. Работа с подстановками
3.6.1. Функциональные преобразования подвыражений
Нередко бывает необходимо заменить некоторое подвыражение в заданном выражении на функцию от этого подвыражения, т.е. осуществить подстановку. Средства для обеспечения подстановок есть во всех СКМ. Так, для этого в Maple 9.5 можно воспользоваться функцией applyop:
• applyop(f, i, е) — применяет функцию f к i-му подвыражению выражения е;
• applyop(f, i, е…, xk,…) — применяет функцию f к i-му подвыражению выражения е с передачей необязательных дополнительных аргументов xk.
Ниже даны примеры применения этой функции (здесь и далее см. файл subs):
> restart;applyop(sin,2,a+x);
> applyop(f,1,g,2,a+b);
> applyop(f,{2,3},a+x+b);
> applyop(f,{1,2},x/y+z);
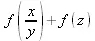
> р:=у^2-2*у-3;
> applyop (f, 2,p);
> applyop{f,[2, 3 ], p);
> applyop(f,{[2,1],3},p);
> applyop(abs,{[2,1],3},p);
3.6.2. Функциональные преобразования элементов списков
Еще две функции, реализующие операции подстановки, указаны ниже:
map(fcn, expr, arg2, ..., argn)
map2(fcn, arg1, expr, arg3,..., argn)
Здесь fcn — процедура или имя, expr — любое выражение, argi — необязательные дополнительные аргументы для fcn.
Первая из этих функций позволяет приложить fcn к операндам выражения expr. Приведенные ниже примеры иллюстрируют использование функции map:
> f:=х->х^2;
> map(f, [1,2,3]);
> map(f,[x,y,z]);
> map(х->х^n, [1,2,3]);
> L:=[1,2,3,4];
> map(proc(x,y) x*y+1 end,[1, 2, 3, 4], 2);
> map(int,L,x);
> map(F, [1, 2, 3], x, y, z);
Из этих примеров нетрудно заметить, что если второй параметр функции map — список, то функция (первый параметр) прикладывается к каждому элементу списка, так что возвращается также список. Из последнего примера видно, что если за вторым параметром идет перечисление аргументов, то они включаются в список параметров функции.
Функции map2 отличается иным расположением параметров. Ее действие наглядно поясняют следующие примеры:
> map2(w, g, {а,b,с});
> map2(op,1,[a+b+i,c+d+k, e+f+j]);
> map2(ор,3,[a+b+i,c+d+k,e+f+j]);
> map2(diff,[sin(х),cos(х),x^n],х);
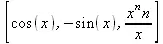
При решении некоторых задач оптимизации возникает необходимость в создании выражений с множителями Лагранжа. Для этого можно использовать список из трех элементов выражения, заключенный в угловые скобки:
> е := <���х^2, -sqrt(16-х^2), 5>;
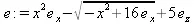
Примеры на работу с выражениями, имеющими множители Лагранжа можно найти в файле демонстрационным L4lagra.mse.
3.6.3. Подстановки с помощью функций add, mul и seq
Заметим, что операции, подобные описанным выше, Maple реализует и с рядом других функций. Ограничимся примерами на подстановки с помощью функций сложения add, умножения mul и создания последовательностей seq:
> add(i,i=[a,b,c]);
> addi=[a,b,c]);
> add(i^2,i=[1,2,3]);
> mul(x-i,i=0..4);
> mul(х^i,i=0..4);
> seq(w(i),i={a,b,c});
> seq(w(x, y, z), i={1,2,3});
> seq(int(x^i,x),i={1,2,3,4});
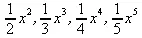
3.6.4. Подстановки с помощью функций subs и subsop
Подстановки в общем случае служат для замены одной части выражения на другую. Частными видами подстановок являются такие виды операций, как замена одной переменной на другую или замена символьного значения переменной ее численным значением. Основные операции подстановки выполняют следующие функции:
• subs(x=a,e) — в выражении е заменяет подвыражение х на подвыражение а;
• subs(s1,…,sn,e) — в выражении е заменяет одни подвыражения на другие, выбирая их из списков s1, sn вида х=а;
• subsop(eq1, eq2, …, eqi, …, eqn, e) — в выражении e заменяет указанные в eqi операнды другими, указанными в правой части равенств eqi вида ni=ei, где ni — номер операнда, ei — выражение для замены.
Все эти функции возвращают измененное после подстановки выражение. Ниже показаны примеры применения функций подстановок:
> subs(а=b,b^2-2*а*b-b^2);
> subs (а=2,b=1,b^2-2*а*b-b^2);
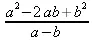
> normal(%);
> subs(a=x,b=y,c=z,[a,b,с]);
> subs({x=y,y=x),[x,y]);
> subs(a=sin(x),b=cos(x),а^2+b*b);
> simplify(%);
> subsop(1=x,a+b+c);
> subsop(2=x,a+b+c);
> subsop(3=x,a+b+c);
> subsop(3=x,a+b/c);
Error, improper op or subscript selector
> subsop(1=sin(x),(1+cos(x))/b);
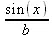
> subsop(2=sin(x),(1+cos(x))/b);
> subsop(1=sin(x),2=sin(x),(1+cos(x))/b);
Следует обратить внимание на то, что результат подстановок, полученный с помощью функции subop, порой может не совпадать с ожидаемым. Поэтому полезно контролировать получаемые в результате подстановок выражения на их корректность.
Одним из важных применений подстановок является проверка правильности решений уравнений и систем уравнений. Ниже дан пример такой проверки:
> eqs:={x+y+z=6,y/x=z-1,z-x=2};
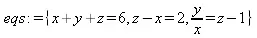
> res:=solve(eqs,{х,у,z});
> subs(res,eqs);
Интервал:
Закладка:










