Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Полезен также параметр symbolic, задающий формальные символьные преобразования для многозначных функций, например, таких как квадратный корень (примеры из файла simplify):

> g:=sqrt(х^2);

> simplify(g);

> simplify(g,assume=real);

> simplify(g,assume=positive);

> simplify(g,symbolic);

Но, чуть иначе:

> g:=sqrt(х^у);

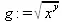
> simplify(g);

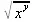
> simplify(g,assume=real);

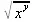
> simplify(g,assume=positive);

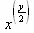
> simplify(g,symbolic);

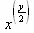
Возможно также применение функции simplify в форме simplify[] где — одно из следующих указаний: atsign, GAMMA, hypergeom, power, radical, RootOf, sqrt, trig.

Ниже даны примеры применения функции simplify:

> simplify(4^(1/2)+3);

> simplify((х^у)^z+3^(3),power);

> simplify(sin(х)^2+cos(х)^2,trig);

> e:=cos(х)^5+sin(х)^4+2*cos(х)^2-2*sin(х)^2-cos(2*х);

> simplify(e);

> simplify(GAMMA(n+4)/GAMMA(n),GAMMA);

> r:=RootOf(х^2-2=0,х):

> simplify(r^2,RootOf);

> simplify(1/r,RootOf);

> simplify(ln(x*y),power,symbolic);

> е:=(-5*b^2*а)^(1/2);

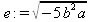
> simplify(e,radical);

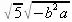
> simplify(e,radical,symbolic);

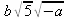
> simplify(GAMMA(n+1)/n!);

Действие функции simplify существенно зависит от областей определения переменных. В следующем примере упрощение выражения не произошло, поскольку результат этой операции неоднозначен:

> restart;

> simplify(sqrt(х^4*у^2));

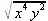
Однако, определив переменные как реальные или положительные, можно легко добиться желаемого упрощения:

> simplify(sqrt(х^4*у^2),assume=positive);

> simplify(sqrt(х^4*у^2),assume=real);

С помощью равенств можно задать свои правила преобразования, например:

> eq:=x^2+2*x*y+y^2;

> simplify(eq,{х=1));

> simplify(eq,{х^2=х*у, у^2=1});

> simplify(eq,{х,у});

Обратите внимание на то, что указание в списке равенств только левой части равенства означает, что правая часть принимается равной нулю. Если функция simplify не способна выполнить упрощение выражения expr, то она просто его повторяет. Это сигнал к применению опций, уточняющих преобразования.

Сложность упрощаемых выражений зависит от объема ОЗУ и вида интерфейса. Очень большие выражения надо разбивать на подвыражения и работать с ними раздельно.

Даже в жизни мы говорим: «не все так просто». Порою упрощенное выражение скрывает его особенности, знание которых является желательным. В этом случае можно говорить о полезности расширения или раскрытия выражения. Функция expand «расширяет» выражение expr и записывается в виде

expand(expr, expr1, expr2, ..., exprn)

где expr — расширяемое выражение, expr1, expr2, …, exprn — необязательные подвыражения — опции. Имеется также инертная форма данной функции — Ехpand(expr). Кроме того, возможно применение операторной конструкции frontend(expans,[expr]).

Функция expand раскладывает рациональные выражения на простые дроби, полиномы на полиномиальные разложения, она способна раскрыть многие математические функции, такие как sin, cos, tan, sinh, cosh, tanh, det, erf, exp, factorial, GAMMA, ln, max, min, Psi, binomial, sum, product, int, limit, bernoulli, euler, abs, signum, pochhammer, polylog, BesselJ, BesselY, BesselI, BesselK, AngerJ, Beta, Hankel, Kelvin, Struve, WeberE и функция piecewise. С помощью дополнительных аргументов expr1, expr2, …, exprn можно задать расширение отдельных фрагментов в expr.

Примеры применения функции expand приведены ниже (файл expand):

> expand((х+2)*(х+3)*(х+4));

> expand(sin(2*х));

> expand(sin(х+у));

> expand([(a+b)*(a-b),tan(2*x)]);

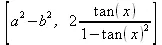
> expand((a+d)*(b+d)*(c+d));

> expand((х+1)*(y+1));

> expand((у+1),(х+1));

> expand( (х+1) *(у+z));

> expand((х+1)*(y+z), х+1);

> frontend(expand,[(a+b)^3]);

Для разложения целых или рациональных чисел на множители в виде простых чисел служит функция

ifactor(n)

или

ifactor(n,method)

где n — число, method — параметр, задающий метод разложения. Другая библиотечная функция, ifactors(n), возвращает результат разложения в форме вложенных списков (файл factor):

> ifactor(123456789);

> ifactor(30!);

> ifactor(12!/20!);

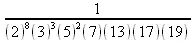
> ifactor(100/78);

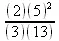
> readlib(ifactors):

> ifactors(100/78);

Для алгебраических выражений функция факторизации записывается в вычисляемой и невычисляемой (инертной) формах:

factor(a)

Factor(a)

factor(a,K)

Factor(a,K)

Здесь а — полином с несколькими переменными, К — необязательное алгебраическое расширение. Для получения результата от инертной формы функции факторизации надо использовать функции вычисления evala или evalgf.

Главная цель факторизации — это нахождение максимального числа независимых сомножителей выражения, линейных по заданным переменным с коэффициентами наиболее простой формы. Ниже представлены примеры применения функции factor:

> factor(а^2+2*а*b+b^2);

> factor(а^2-2*а*b-b^2);

> p:=expand((х-1)*(х-2)*(х-3)*(х-4));

> factor(р);

> factor(х^5-2,2^(1/5));

> alias(alpha=RootOf(х^2-2));

> factor(х^2-2,alpha);

> factor(х^3-у^3);

> factor(х^3-у^3, (-2)^(1/2));

> factor(х^3-у^3, (-3)^(1/2));