Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
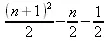
> sum(i/(i+1),i=0..n);
> sum(k*binomial(n,k),k=0..n);
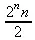
Некоторые из таких сумм выражаются через специальные математические функции.
4.1.4. Суммы бесконечных рядов
Многие суммы бесконечных рядов сходятся к определенным численным или символьным значениям, и система Maple способна их вычислять. Это поясняют следующие примеры (файл sum):
> restart;
> sum(-exp(-k), k);
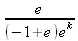
> sum(k*a^k,k);
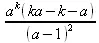
> sum(1/k!,k=0..infinity);
> Sum(1/i^2, i=1..infinity) = sum(1/i^2, i=1..infinity);
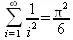
> Sum(1/n!, n=1..infinity) = sum(1/n!, n=1..infinity);
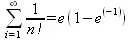
> evalf(%);
> Sum(1/i^2, i)=sum(1/i^2, i);
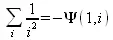
4.1.5. Двойные суммы
Могут встречаться множественные суммы по типу «сумма в сумме». Ограничимся приведением примера двойной суммы, имеющей аналитическое значение (файл sum):
> Sum(Sum(k^2, k = 1..m), m = 1..N); factor(simplify(value(%)));
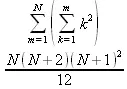
При конкретном значении N такую сумму нетрудно вычислить подстановкой:
> subs(N = 100, %);
Как видно из приведенных примеров, средства вычисления сумм последовательностей Maple 9.5/10 позволяют получать как численные, так и аналитические значения сумм, в том числе представляемые специальными математическими функциями.
4.1.6. Пакет вычисления специальных сумм sumtools
Возможности вычисления специальных сумм существенно расширяются при использовании инструментального пакета вычисления специальных сумм sumtools. При его вызове выводится список функций пакета:
> with(sumtools);
Назначение функций данного пакета перечислено ниже:
hypersum(U, L, z, n) и Hypersum(U, L, z, n) — вычисление гиперсумм;
sumtohyper(f, k) и Sumtohyper(f, k) — преобразование сумм в гиперсуммы;
extended_gosper(f, k), extended_gosper(f, k=m..n) и extended_gosper(f, k, j) — реализация расширенного алгоритма Госпера;
gosper(f, k) и gosper(f, k=m..n) — реализация алгоритма Госпера;
hyperrecursion(U, L, z, s(n)) — реализация гиперрекурсионного алгоритма;
hyperterm(U, L, z, k) и Hyperterm(U, L, z, k) — ввод гипергеометрического терма.
4.1.7. Примеры вычисления специальных сумм
Приведем примеры на вычисление специальных сумм с помощью функций пакета sumtools (файл sumtools):
> extended_gosper(k*(k/2)!, k);
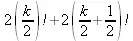
> extended_gosper(k*(k/2)!,k,2);
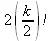
> extendedgosper(k*(k/2)!,k=1..n);
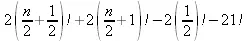
> gosper(k*(k/2)!,k);
> gosper(pochhammer(k,n),k);
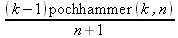
> hyperrecursion([-n,a],[b],1,f(n));
> Hypersum([a,1+a/2,b,c,d,1+2*a-b-c-d+n, -n],
[a/2,1+a-b,1+a-c,1+a-d,1+a-(1+2*a-b-c-d+n),1+a+n],1,n);
> simpcomb(binomial(n,k));
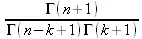
> sumrecursion(binomial(n,k)^3,k, f(n));
> hyperterm([a,b], [c],z,k);
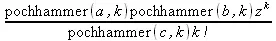
Из этих примеров применение функций данного пакета достаточно очевидно.
4.2. Вычисление произведений членов последовательностей
4.2.1. Основные функции для произведения членов последовательностей
Аналогичным образом для произведений членов f(i) некоторой последовательности, например вида
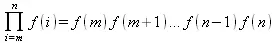
используются следующие функции:
product(f, k);
product(f, k=m..n);
product(f, k=alpha);
Product(f, k);
Product(f, k=m..n);
Product(f, k=alpha).
Обозначения параметров этих функций и их назначение соответствуют приведенным для функций вычисления сумм. Это относится, в частности, и к применению одиночных кавычек для f и k.
4.2.2. Примеры вычисления произведений членов последовательностей
Примеры применения функций вычисления произведений даны ниже (файл product):
> restart;
> Product(k^2,k=1..5)=product(k^2, k=1..5);
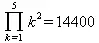
> Product(k^2, k)=product(k^2,k)
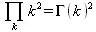
> product(а[k],k=1..5);
> f:= [1, 2, 3, 4, 5];
> product(f[k],k=1..4);
> product(n+k,k=1..4);
> Product(n+k,k=1..m)=product(n+k,k=1..m);
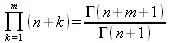
> product(k,k=RootOf(x^3-9));
Как и в случае вычисления сумм, вычисление произведений возможно как в численной, так и в аналитической форме — разумеется, если таковая существует. Это показывают следующий пример:
> Product(2/i,i=1..infinity)=product(2/i,i=1..infinity);
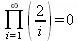
Нетрудно понять, что при i, стремящемся к бесконечности, перемножаемые члены последовательности стремятся к нулю, а потому к нулю стремится и их произведение.
4.3. Вычисление производных
4.3.1. Определение производной и полного дифференциала
Если f(x ) непрерывная функция аргумента х , то производная этой функции
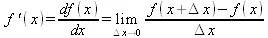 (4.1)
(4.1)
Как известно, значение производной геометрически характеризуется наклоном касательной к графику f(х) в точке x=0. Простейший способ наблюдать построение касательной к заданной точке функции заключается в применении функции showtangent из пакета student. Например, команды
Читать дальшеИнтервал:
Закладка:










