Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> convert([a,b,с,d],`+`);

> f:=seq(x[i]^n,i=1..4);

> x:='x'; convert(sinh(x),ехр);

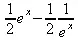
> convert(1.234567,fraction);

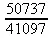
> convert(1/7,float);

> convert(sin(I*x),exp);

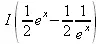
> convert(sinh(x),exp);

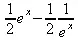
> convert(arcsinh(x),ln);

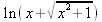
> convert(12345,list);

> convert(binomial(m,n),factorial);

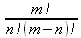
> convert([[1,2],[3,4],[5,6]],table);

> convert(-Pi,signum);

> s:=taylor(sin(x),x,8);

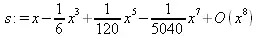
> p:=convert(s,polynom);

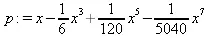
> convert(p,float);

> f:=(х^4+х)/(x^2-1);

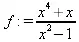
> convert(f, parfrac, x);

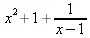
> s:=series(f,x,5);

> convert(s,polynom);# Удаление члена ряда, описывающего погрешность

Из этих примеров (их список читатель может пополнить самостоятельно) следует, что функция преобразования convert является одной из самых мощных функций Maple. С ее помощью можно получить множество различных форм одного и того же выражения.

Еще одним мощным средством преобразования выражений является функция combine. Она обеспечивает объединение показателей степенных функций и преобразование тригонометрических и некоторых иных функций. Эта функция может записываться в трех формах:

combine(f)

combine(f, n)

combine(f, n, opt1, opt2,...)

Здесь f — любое выражение, множество или список выражений; n — имя, список или множество имен; opt1, opt2, … — имена параметров. Во втором аргументе можно использовать следующие функции:

@@ abs arctan conjugate ехр

ln piecewise polylog power product

Psi radical range signum trig

Примеры применения функции combine представлены ниже (файл expr1):

> combine(ехр(2*х)^2,ехр);

> combine(2*sin(х)^2+2*cos(х)^2);

> combine(sin(х)*cos(х));

> combine(Int(х,x=a..b)-Int(х^2,x=a..b));

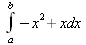
Эти примеры далеко не исчерпывают возможности функции combine в преобразовании выражений. Рекомендуется обзорно просмотреть примеры применения функции combine с разными параметрами, приведенные в справочной системе Maple.

Выражения и их части в Maple рассматриваются как объекты. В ходе манипуляций с ними важное значение имеет контроль за типом объектов. Одной из основных функций, обеспечивающих такой контроль, является функция whattype(object), возвращающая тип объекта, например string, integer, float, fraction, function и т.д. Могут также возвращаться данные об операторах. Примеры применения этой функции даны ниже (файл control):

> whattype(2+3);

> whattype(Pi);

> whattype(123./5);

> whattype(1/3);

> whattype(sin(x));

> whattype([1, 2, 3, a, b, c]);

> whattype(a+b+c);

> whattype(a*b/c);

> whattype(a^b);

> whattype(1+2+3=4);

С помощью функции type(object,t) можно выяснить, относится ли указанный объект к соответствующему типу t, например:

> type(2+3,integer);

> type(sin(х),function);

> type(hello,string);

> type("hello",string);

> type(1/3,fraction);

При успешном соответствии типа объекта указанному (второй параметр), функция type возвращает логическое значение true, в противном случае — false.

Для более детального анализа объектов может использоваться функция hastype(expr, t), где expr — любое выражение и t — наименование типа подобъекта.

Эта функция возвращает логическое значение true, если подобъект указанного типа содержится в выражении expr. Примеры применения этой функции даны ниже (файл control):

> hastype(2+3,integer);

> hastype(2+3/4,integer);

> hastype(2*sin(x),function);

> hastype(a+b-c/d,`+`);

Еще одна функция — has(f,x) — возвращает логическое значение true, если подобъект х содержится в объекте f, и false в ином случае:

> has(2*sin(х),2);

> has(2*sin(x), `/`);

> has(2*sin(x),3-1);

Следует отметить, что соответствие подобъекта выражения указанному подобъекту понимается в математическом смысле. Так, в последнем примере подобъект «3-1», если понимать его буквально, в выражении 2*sin(x) не содержится, но Maple-язык учитывает соответствие 3-1=2, и потому функция has в последнем примере возвращает true.

Функция has может использоваться для выявления той или иной математической операции, оператора или функции. Однако надо соблюдать определенные правила, поскольку выражение, анализируемое функцией has оценивается и исполняется. Внимательно проанализируете приведенные ниже примеры:

> has(2*sin(2),sin);

> has(2*sin(2),'sin');

> has(2*sin(2.), 'sin');

Здесь надо учесть, что выражение 2*sin(2) после оценки и исполнения не меняется, поскольку Maple, при целочисленном аргументе функции синуса, не вычисляет ее и вычисленное выражение совпадает с исходным и содержит функцию синуса. Однако sin(2.) уже вычисляется и становится числом. Именно поэтому в последнем примере функция sin уже не обнаруживается. Подобное имеет место и в ряде других примеров с функцией интегрирования:

> has('int(х^2,х)',int);

> has(int(х^2,х),int);

> int(х^2,х);

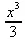
> has(int(х^2,х), х^3/3);rue

Столь же поучителен пример с идентификацией функции интегрирования. Так, has(int(х^2, х), int); дает false, поскольку интеграл оценивается и вычисляется, что ведет к подмене выражения на х^3/3 уже не содержащего признаков интегрирования. Это и поясняют два последних примера, в которых вычислено значение интеграла и функция has дает значение true для значения интеграла. В тоже время заключение int(x^2,x) в апострофы позволяет найти имя функции интегрирования int, поскольку исходное выражение в этом случае представлено в неисполняемой форме и содержит обращение к этой функции.