Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> polar(z);

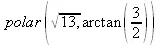
> polar(-3.,Pi/2);

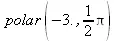
В некоторых случаях полезна визуализация операций с комплексными числами. Для этого удобен пакет расширения plots, который позволяет представлять комплексные числа в виде стрелок на комплексной плоскости. Например, для иллюстрации операции умножения двух комплексных чисел

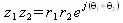
можно использовать следующие графические построения (файл complpot):

> with(plottools):

l1 := arrow([0,0], [1,2], .1, .3, .1, color=green):

l1a := arc([0,0],1.5,0..arctan(2),color=green):

> l2 := arrow([0,0], [1,-8], .1, .3, .1, color=green):

l2a := arc([0,0],.75,0..arctan(.8),color=green):

> l3 := arrow([0,0], [-.6,2.8], .1, .3, .1, color=black):

l3a := arc([0,0],2.5,0..arctan(2.8,-.6),color=black):

> plots[display](l1,l2,l3,l1a,l2a,l3a, axes=normal,view=[-3..3,0..3],scaling=constrained);

Они создают график (рис. 3.11) наглядно иллюстрирующий операцию перемножения двух комплексных чисел, представленных своими радиус-векторами.

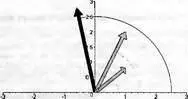
Рис. 3.11. Иллюстрация перемножения двух комплексных чисел

При изучении графиков элементарных функций вне особенностей системы Maple полезно Maplet-приложение, окно которого представлено на рис. 3.12. Открывается это окно исполнением команды Tools→Precalcus→Standard Functions… при работе в стандартном интерфейсе Maple 9.5.

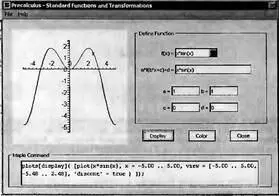
Рис. 3.12. Maplet-окно для изучения функций и построения их графиков

В окне в разделе определения функций Define Function имеется список элементарных функций, графики которых можно просматривать. Однако, возможно построение и графиков простых функций более сложного вида, например x*sin(x) вместо sin(x) — это и иллюстрирует график, представленный на рис. 3.12. Maplet-окно генерирует команду на Maple-языке, которая строит график заданной функции.

Специальные математические функции являются решениями дифференциальных уравнений, которые невозможно представить через элементарные функции. Через такие функции нередко представляются и многие интегралы. Наиболее мощные из СКМ, например Maple, широко используют специальные математические функции в ходе символьных преобразований. Рассмотрим наиболее важные специальные математические функции.

Функция Эйри формирует пару линейно независимых решений дифференциального уравнения вида:

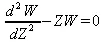
Связь между функцией Эйри и модифицированной функцией Бесселя выражается формулой:

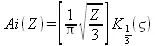
где

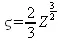
Дифференциальное уравнение вида

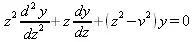
где v — неотрицательная константа, называется уравнением Бесселя, а его решения известны как функция Бесселя. J(z)и J _ (z)формируют фундаментальное множество решений уравнения Бесселя для неотрицательных значений (так называемые функции Бесселя первого рода):

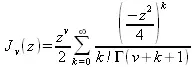
где для гамма-функции используется следующее представление:

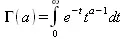
Второе решение уравнения Бесселя, линейно независимое от J(z), определяется как

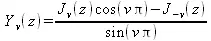
и задает функции Бесселя второго рода Y(z).

Функции Бесселя третьего рода (функции Ханкеля) и функция Бесселя связаны следующим выражением:

H (1) v ( z ) = J v ( z ) + iY v (z),

H (2) v ( z ) = J v ( z ) - iY v (z).

Дифференциальное уравнение вида

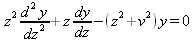
где v — неотрицательная константа — называется модифицированным уравнением Бесселя, и его решения известны как модифицированные функции Бесселя I(z)и I _ (z). K(z)— второе решение модифицированного уравнения Бесселя, линейно независимое от I(z). I(z)и K(z)определяются как:

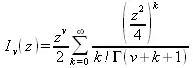
и

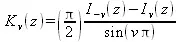
Бета-функция определяется как:

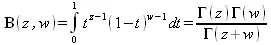
где Г(z) — гамма-функция. Неполная бета-функция определяется интегральным выражением:

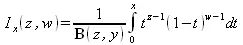
Эллиптические функции Якоби определяются интегралом:

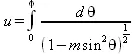
В некоторых случаях при определении эллиптических функций используются модули k вместо параметра m. Они связаны выражением:

k² = m = sin² α.

Полные эллиптические интегралы первого и второго рода определяются следующим образом:

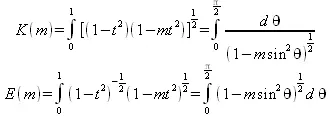
Функция ошибки (интеграл вероятности) определяется следующим образом:

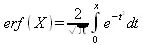
erf(X)— возвращает значение функции ошибки для каждого элемента вещественного массива X.

Остаточная функция ошибки задается соотношением:

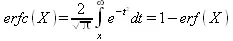
Встречается и масштабированная остаточная функция ошибки. Эта функция определяется так: