Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

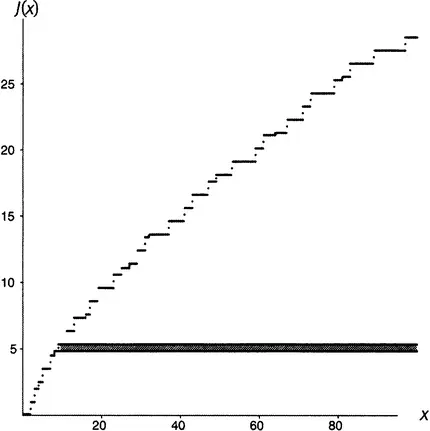
Рисунок 19.4. .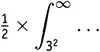

Конечно, площадь под графиком функции J бесконечна. Нарисованная полоска уже имеет бесконечную площадь (высота 1/ 2, длина бесконечна, площадь 1/ 2×∞ = ∞). Таковы же площади и всех других полосок. Все вместе они складываются в бесконечность. Но что, если я пожелаю «придавить» функцию J справа таким образом, чтобы площадь под графиком стала конечной? Так, чтобы каждая из этих полосок постепенно сужалась и сжималась до такой степени, чтобы площадь ее стала конечной? Как можно было бы осуществить такое «придавливание»?

Последний интеграл подсказывает как. Предположим, что мы взяли какое-нибудь число s (которое будем считать большим единицы). Для каждого аргумента x умножим J(x) на x − s −1. Для иллюстрации возьмем s = 1,2. Тогда x − s −1= x −2,2или, другими словами, 1/ x 2,2. Возьмем аргумент x , скажем, равным 15. Вот, J (15) есть 7,333333…, а 15 −2,2равно 0,00258582…. Перемножая, получаем, что J(x)x − s −1имеет значение 0,018962721…. Если брать большие аргументы, то сдавливание будет выражено более ярко. При x = 100 значение выражения J(x)x − s −1равно 0,001135932….

На рисунке 19.5 показан график функции J(x)x − s −1при s = 1,2. Чтобы подчеркнуть «эффект сдавливания», там показана та же самая полоска, которая была выделена и ранее, но теперь после сдавливания. Видно, как она все более и более худеет по мере того, как аргумент устремляется на восток. Имеется вполне реальный шанс, что вся площадь окажется конечной, несмотря на свою бесконечную длину. В предположении, что так и есть и что дело обстоит таким же образом для всех полосок, спросим себя: какова же будет полная площадь под графиком этой функции? Или, выражаясь математически, каково будет значение ?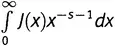

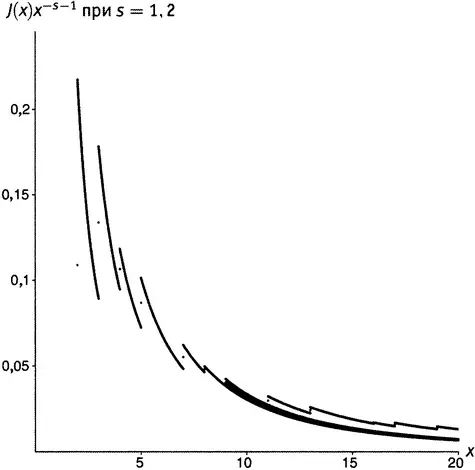
Рисунок 19.5. 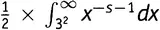при s = 1,2.

Давайте посмотрим. Будем перебирать простые числа одно за одним. Для простого числа 2 до сдавливания имеем полоску высоты 1, идущую от 2 до бесконечности, далее полоску высоты идущую от 2 2до бесконечности, затем полоску высоты идущую от 2 3до бесконечности, и т.д. Сумма площадей сдавленных полосок — если мы рассматриваем пока только простое число 2 — равна (19.4):

Конечно, это пока только 2-полоски. Имеется аналогичная бесконечная сумма интегралов для 3-полосок (19.5):

И аналогичная сумма для 5, потом для 7 и т.д. для всех простых чисел. Бесконечная сумма бесконечных сумм интегралов! Все хуже и хуже! Да, но самый густой мрак перед рассветом.

Это возвращает нас к началу данного раздела. Поскольку интеграл прозрачен для умножения на число , — это то же самое, что 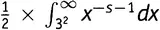. Но в начале раздела мы видели, что член, который мы в качестве пробного выбрали в выражении (19.3), т.е. 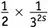, равен 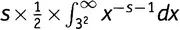— другими словами, s умножить на то, что мы только что получили. Так к чему же сводится выражение (19.5)? Вот именно, в точности ко второй строке в выражении (19.3), деленной на s ! А выражение (19.4)плюс выражение (19.5)плюс аналогичные выражения для всех остальных простых чисел суммируются к выражению (19.3), деленному на s . Вот и рассвет! Получается, что штука, с которой я тут забавляюсь, т.е. , равна просто выражению (19.3), деленному на s . Но выражение (19.3)равно ln ζ(z) , как нам подсказывает Золотой Ключ. Отсюда получается следующий результат.

Я просто не нахожу слов, чтобы выразить, насколько это чудесный результат. Он ведет прямо к центральному результату в работе Римана — результату, который будет предъявлен в главе 21. На самом деле это просто переписывание Золотого Ключа в терминах анализа. Однако переписать его так — это невероятно мощное достижение, потому что теперь Золотой Ключ открыт для всех мощных средств дифференциального и интегрального исчисления XIX века. В этом состояло достижение Римана.

Среди упомянутых средств обращения имеется еще один метод, который позволяет вывернуть полученное выражение наизнанку и записать J через ζ . Я немного потяну с предъявлением обращенного выражения. Но логика во всяком случае ясна:

• можно выразить π(x) через J(x) (раздел IV данной главы);

• обратив выражение (19.6), можно выразить J(x) через дзета-функцию

и, следовательно,

• можно выразить π(x) через дзета-функцию.

Именно за это предприятие Риман и взялся, потому что в результате окажется, что все свойства функции π некоторым образом закодированы в свойствах ζ -функции.

Функция π относится к теории чисел; ζ -функция относится к анализу, и мы перебросили понтонный мост через пролив, разделяющий два берега — счет и измерение. Коротко говоря, мы только что получили мощный результат в аналитической теории чисел. На рисунке 19.6 графически представлено выражение (19.6) — Золотой Ключ в аналитическом виде.

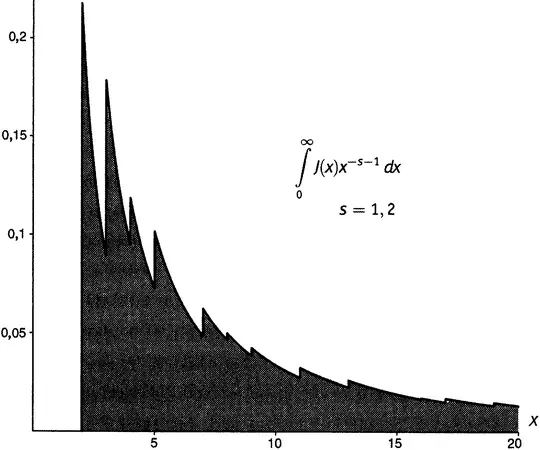
Рисунок 19.6.Затемненная область представляет собой интеграл 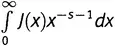при s = 1,2. Его численное значение составляет 1,434385276163. Он равен 1/ s ∙ln ζ(s).

Закон Монтгомери-Одлыжко утверждает, что нетривиальные нули дзета-функции Римана выглядят — имеется в виду статистически — как собственные значения некоторой случайной эрмитовой матрицы. Операторы, представляемые такими матрицами, можно использовать для моделирования определенных динамических систем в квантовой физике. А имеется ли при этом оператор Римана — оператор, собственные значения которого в точности совпадают с нулями дзета-функции? Если да, то какую динамическую систему он представляет? Удастся ли создать такую систему в физической лаборатории? И если удастся, то поможет ли это в доказательстве Гипотезы?