Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Эти вопросы активно изучались еще до выхода статьи Одлыжко 1987 года. За год до того Майкл Берри опубликовал статью под заглавием «Дзета-функция Римана: Модель квантового хаоса?». Используя ряд хорошо известных и широко обсуждавшихся в то время результатов (и среди них некоторые результаты Одлыжко), Берри обратился к следующему вопросу. Предположим, что риманов оператор существует; тогда динамическую систему какого типа он бы моделировал? Ответ, который он предложил, — хаотическую систему. Чтобы объяснить это, нам надо ненадолго переключиться на знакомство с теорией хаоса.

Тот факт, что чистая теория чисел — наука о натуральных числах и их взаимоотношениях — может соотноситься с субатомной физикой, вовсе не удивителен. В квантовой физике арифметическая составляющая выражена намного сильнее, чем в классической физике, поскольку основополагающая идея состоит в том, что материю и энергию нельзя делить до бесконечности. Энергия передается только в виде 1, 2, 3 или 4 квантов, но никак не 1 1/ 2, 2 17/ 52, √2 или π квантов. Это, конечно, далеко не все, что есть в квантовой механике; ее саму невозможно было бы разработать без наиболее мощных средств самого современного анализа. Например, знаменитое волновое уравнение Шредингера записывается на традиционном языке дифференциального исчисления. Тем не менее арифметическая составляющая в квантовой механике несомненно присутствует, тогда как в классической механике ее практически вовсе нет.

Основания классической физики — физики Ньютона и Эйнштейна — по сути своей аналитические, в математическом смысле. Они опираются на математический анализ, на понятия бесконечной делимости, гладкости и непрерывности, предела и производной, а также вещественных чисел. Не будем забывать, что, именно развивая и доводя понятие «предела» до логического конца, Ньютон и изобрел дифференциальное и интегральное исчисление, в конце концов ставшее содержанием большей части анализа.

Рассмотрим классическую задачу о движении одного тела вокруг другого по эллиптической орбите под действием силы их взаимного гравитационного притяжения. На некотором расстоянии (измеряемом вещественным числом r ) от основного тела другое тело (спутник) имеет некоторую строго определенную скорость (выражаемую другим вещественным числом v ). Связь между v и r дается точным математическим выражением; v есть в действительности функция от r , выражаемая так называемым уравнением vis viva [179], знакомым всем, кто изучал элементарную небесную механику:

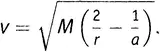
где M и a — некоторые заданные числа, определяемые параметрами системы и начальными условиями — в частности, массами тел и т.п.

На практике, конечно, нельзя достичь бесконечной точности, требуемой для того, чтобы присвоить определенные вещественные значения величинам r и v. Пусть даже мы измеряем r с точностью до 10 или даже 20 знаков после запятой; но ведь для точного выражения вещественного числа требуется бесконечно много десятичных разрядов, а добиться такого мы не можем. Следовательно, для любой реальной орбиты имеется некоторая, пусть очень малая, ошибка при определении вещественных значений буквы r , а также соответствующая ошибка в вычисленных значениях буквы v . Это не играет большой роли: законы Кеплера уверяют нас, что все равно получится правильный эллипс, а математика уравнения vis viva говорит, что ошибка в 1 процент при определении r , как правило, приведет лишь к 0,5-процентной ошибке при вычислении значений v. Таким образом, ситуация управляема и предсказуема. Как говорят математики, «задача интегрируема».

Но это была очень простая задача. Почти все реальные физические проблемы сложнее, чем эта. Рассмотрим, например, случай трех тел, испытывающих взаимное гравитационное притяжение, — знаменитую «задачу трех тел». Можно ли найти ее решение в замкнутом виде, как для уравнения vis viva ? Интегрируема ли она?

К концу XIX столетия стало ясно, что ответы таковы: «нет, не можем» и «нет, задача неинтегрируема». Единственный способ получить решение — использовать численные расчеты на компьютере, которые неизбежно носят приближенный характер.

На самом деле в 1890 году Анри Пуанкаре опубликовал статью, внесшую ясность в задачу трех тел: он четко показал, что эта задача не только не допускает решения в замкнутом виде, но и обладает куда более тревожным свойством — ее решения временами приобретают хаотический характер. Это значит, что даже малейшие изменения начальных условий в задаче — аналогов величин M и a в рассмотренном примере задачи двух тел — могут привести к изменению вычисленных орбит до неузнаваемости. Сам Пуанкаре заметил, что один набор условий дает «орбиты столь запутанные, что я даже и не пытался их изобразить».

Согласно распространенному мнению, работа Пуанкаре знаменует собой рождение современной теории хаоса. В течение нескольких десятилетий в теории хаоса не происходило ничего особенного, главным образом потому, что у математиков просто не было средств для обращения с числами — средств для перемалывания чисел в масштабах, требуемых при анализе хаоса. Ситуация изменилась, когда стали доступными компьютеры, и теория хаоса пережила второе рождение в 1960-х годах в трудах метеоролога Эда Лоренца, работавшего в Массачусетсом технологическом институте. [180]Теория хаоса в настоящее время представляет собой обширный предмет, охватывающий много различных более частных дисциплин из физики, чистой математики и вычислительной математики.

Важно осознать, что такая хаотическая система, как решение задачи трех тел, не обязана состоять из случайных движений (и, как правило, из них и не состоит). Прелесть теории хаоса заключается в том, что в хаотических системах присутствуют определенные структуры. В общем случае хаотическая система никогда не проходит снова по раз пройденным положениям, однако она повторяющимся образом воспроизводит указанные структуры; в их основе лежат некоторые правильные, но неустойчивые периодические орбиты, по которым система теоретически могла бы двигаться, если бы нам была доступна бесконечная точность, требуемая для запуска системы именно и абсолютно точно по такой орбите.

При первом появлении современной теории хаоса физики восприняли ее как чисто классический предмет, не имеющий никакого отношения к квантовой теории. Хаос возникает из явлений, подобных тем, какие происходят в задаче трех тел, вследствие того, что начальные условия задаются вещественными числами, числами для измерения, которые можно дробить до бесконечности; их можно изменить на 1 процент, или на 0,1 процента, или на 0,001 процента… Поскольку условия можно варьировать бесконечно, возникает бесконечно много возможных вариантов движения системы. В квантовой же теории, наоборот, начальные условия можно варьировать на 1, 2 или 3 единицы, но не на 1 1/ 2или 2,749. Получается так, что в квантовой теории для хаоса «не должно быть места». Верно, что в квантовой механике имеется некоторая степень неопределенности, но управляющие всем уравнения тем не менее линейны. Малые возмущения приводят к малым последствиям, как это имеет место и для классического уравнения vis viva в задаче двух тел.