Генри Дьюдени - Пятьсот двадцать головоломок

213. Лилавати.Вот небольшая задачка, заимствованная из «Лилавати» (1150 г.) Бхаскары [14] Вводная часть (арифметика) трактата «Венец астрономического учения» выдающегося индийского математика XII в. Бхаскары. — Прим. перев. .

«Прекрасная дева с лучистым взором назвала мне число. Если это число умножить на 3, прибавить ¾ произведения, разделить на 7, уменьшить на уз частного, умножить на себя, уменьшить на 52, извлечь квадратный корень, прибавить 8, разделить на 10, то получится 2».

При правильном подходе решить эту задачу, как и многие другие старинные головоломки, невероятно легко.

214. Задача печатника.Некий печатник получил годовой заказ на 10 000 афиш в месяц. Разумеется, в январе на афише должно было стоять слово «ЯНВАРЬ», а в феврале — «ФЕВРАЛЬ» и т. д. Таким образом, необходимо было напечатать 10 000 афиш с надписью «ЯНВАРЬ», 10 000 афиш с надписью «ФЕВРАЛЬ», 10 000 афиш с надписью «МАРТ» и т. д. Литеры, которыми набирались названия месяцев, отливались по особому заказу и стоили дорого, поэтому печатнику хотелось купить их как можно меньше, чтобы часть литер, использованных при наборе одного месяца, можно было бы использовать и при наборе других месяцев, а запаса хватило бы на все месяцы года.

Сколько различных литер он должен купить? Разумеется, все слова печатаются прописными буквами, как и показано выше.

215. Пчелиный рой.Вот пример изящной формы, в которую уже упоминавшийся выше Бхаскара облек небольшую головоломку.

«Квадратный корень из половины общего количества пчел в рое вылетел на куст жасмина; всего роя осталось на месте; одна пчелка летает вокруг своего возлюбленного, жужжащего внутри лотоса, куда он залетел ночью, привлеченный ароматом этого цветка, который ныне стал его темницей. Скажи мне число пчел в рое».

216. Слепота у летучих мышей.Один натуралист, пытаясь мистифицировать полковника Крэкхэма, сообщил ему, что изучал вопрос о слепоте у летучих мышей.

— Я обнаружил, — сказал он, — что закоренелая привычка летучих мышей спать днем в темных углах и вылетать только по ночам привела к распространению у них слепоты, хотя некоторые особи хорошо видели обоими или одним глазом. Две из исследуемых мною мышей видели правым глазом, три — левым, четыре не видели левым и пять не видели правым глазом.

Могли бы вы подсчитать наименьшее число летучих мышей, которых пришлось осмотреть натуралисту, чтобы получить такие результаты?

217. Зверинец.В бродячем зверинце было два каприза природы: четырехногая птица и шестиногий теленок. Одного посетителя спросили, сколько всего там показывали птиц и животных, на что он ответил:

— Всего 36 голов и 100 ног. Остальное вы можете узнать сами.

Сколько же там было птиц и зверей?

218. Угон овец.Грабители угнали ⅓ стада овец и ⅓ овцы. Другая шайка угнала ¼ оставшихся овец и ¼ овцы. Затем третья шайка грабителей угнала ⅕ остатка и еще ⅗ овцы, после чего в стаде осталось 409 овец.

Сколько овец было в стаде первоначально?

219. Дележ овец.Некий австралийский фермер, умирая, оставил своих овец трем сыновьям. Альфред должен получить на 20% больше, чем Джон, и на 25% больше, чем Чарлз. Доля Джона составляет 3600 овец.

Сколько овец получит Чарлз? Возможно, что читателю удастся решить задачу за несколько секунд.

220. Арифметика в такси.Водитель такси не отличался вежливостью, и возмущенный мистер Уилкинс попросил его назвать свой номер.

— Вы хотите узнать мой номер? — сказал водитель. — Что же, пожалуйста. Если вы разделите его на 2, 3, 4, 5 или 6, то получите в остатке 1, а на 11 он разделится без остатка. Скажу еще, что из всех водителей, которые могли бы сказать о своем номере то же самое, мой номер самый маленький.

Какой номер был у водителя?

221. Аренда.«Как-то я обсуждал со своим другом вопрос об аренде, — сказал полковник Крэкхэм, — и он сообщил мне, что его земля сдана в аренду на 99 лет. Я спросил друга, сколько лет из этого срока уже истекло, надеясь получить прямой ответ. Но он сказал мне, что ⅔ прошедшего времени равны ⅘ оставшегося срока и что ответ я должен найти сам».

222. Походная колонна.Воинское подразделение двигалось походной колонной, в которой число шеренг превышало число солдат в шеренге на 5. Когда показался неприятель, произошло перестроение в 5 шеренг, при этом число солдат в каждой шеренге увеличилось на 845 человек.

Сколько человек было в подразделении?

223. Год 1927.Можно ли найти числа p и q , если p q - q p = 1927? Вот поясняющий пример для случая 1844 г. При p = 3 и q = 7 мы имеем

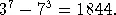
Сумеете ли вы записать число 1927 аналогичным образом?

224. Ящики со снарядами.Снаряды для шестидюймовых гаубиц были упакованы в ящики по 15, 18 и 20 штук.

— Почему у вас разные ящики? — спросил я офицера на складе.

— Видите ли, — ответил он, — это позволяет нам доставлять на батарею нужное количество снарядов, не открывая ящиков.

Действительно, эта система работала безотказно, когда требовалось большое количество снарядов, но оказывалась негодной, если требовалось доставить, например, 5, 10, 25 или 61 снаряд.

Какое наибольшее число снарядов нельзя доставить на батарею целыми ящиками, вмещающими по 15, 18 и 20 снарядов? Оно не слишком велико.

225. Фруктовый сад.Садовник решил разбить новый фруктовый сад. Он посадил молодые деревья рядами таким образом, что получился квадрат. При этом у него осталось 146 лишних саженцев. Но чтобы увеличить квадрат, добавив лишний ряд, садовнику пришлось купить еще 31 дерево. Сколько деревьев стало в саду по окончании работы?

226. Кубики и квадраты.Вот одна интересная, хотя и не простая головоломка, автора которой установить не удалось.

У троих детей было по совершенно одинаковой коробке с кубиками. Первая девочка составила изо всех своих кубиков квадратную рамку, отмеченную на рисунке буквой А .

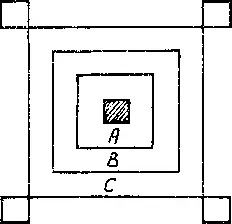
Вторая девочка составила квадрат побольше — В . У третьей девочки получился еще больший квадрат — С , но при этом осталось 4 кубика, которые она разместила по углам, как показано на рисунке. Каждая девочка использовала все свои кубики.

Какое наименьшее число кубиков могло содержаться в каждой коробке? Не следует думать, будто на рисунке соблюдены истинные пропорции между размерами квадратов.

227. Найдите треугольник.Стороны и высота некоторого треугольника выражаются четырьмя последовательными целыми числами. Чему равна площадь этого треугольника?