Генри Дьюдени - Пятьсот двадцать головоломок

246. Бакалейщик должен смешать 70 фунтов чая по 32 цента и 30 фунтов чая по 40 центов за фунт.

247. Рыба весит 72 унции, или 4½ фунта. Хвост весит 9 унций, туловище 36 и голова 27 унций.

248. Ясно, что 999 919 не может быть простым числом и что, поскольку нужно найти единственное решение, оно должно разлагаться в произведение двух простых сомножителей. Этими сомножителями будут 991 и 1009. Нам известно, что каждая кошка поймала больше мышек, чем было кошек. Значит, всего была 991 кошка, и каждая из них поймала по 1009 мышек.

249. Пусть номер ящика равен n . Тогда в нем будет 2 n - 1 перегородок в одном направлении и 2 n - 3 в другом, что даст 4 n 2- 4 n ячеек и 4 n - 4 перегородок. Так, в двенадцатом ящике имеются 23 и 21 перегородок (всего 44) и 528 ячеек. Это правило годится для всех ящиков, кроме второго, где может быть любое количество перегородок в одном направлении и одна перегородка в другом. Так что 1 и 1 подойдут (единственная перегородка не годится, поскольку такое «перегораживание» было бы нелепостью). Таким образом, всего получается 262 перегородки и 2284 ячейки (а не 264 и 2288).

250. Если внутренний диаметр звена умножить на число звеньев и прибавить удвоенную толщину железного прута, то получится длина цепи. Каждое звено, присоединенное к цепи, теряет в своей длине удвоенную толщину прута. Внутренний диаметр равен 2⅓ см. Если мы умножим его на 9 и прибавим 1, то получим ровно 22 см, а если мы умножим его на 15 и прибавим 1, то как раз и получится 36 см. Следовательно, два куска цепи содержат соответственно по 9 и 15 звеньев.

251. Если брат отвечал Доре «чет», то десятицентовая монета находилась в правом кармане, а пятицентовая в левом. Если же он говорил «нечет», то пятицентовая монета лежала в правом, а десятицентовая в левом кармане.

252. Первоначально в каждой сахарнице было по 36 кусков, а после того, как в каждую чашку положили по 2 ( ) куска, в чашках стало по 6, а в сахарницах — по 18 кусков. Разность как раз и равна 12.

253. Всего 51 секция, в каждой секции по 23 целые колонки. Итого получалось 1173 целые колонки и 50 пар половинок, что составляло в совокупности 1223 колонки, как и требовалось по условию задачи.

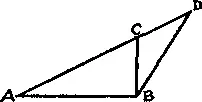
254. Пусть длина AB 10 см. Из точки B восставим к AB перпендикуляр BC , равный половине AB . Соединим точки A и C отрезком прямой и продолжим его за точку C так, чтобы CD = CB . Проведем отрезок BD . Это и есть искомый радиус окружности. Если начертить эту окружность и вписать в нее правильный пятиугольник, то стороны последнего будут точно равны 10 см.

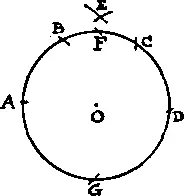
255. Чтобы отметить вершины квадрата с помощью одного циркуля, сначала рисуют круг. Затем, зафиксировав раствор циркуля и начав с любой произвольно взятой на окружности точки A , отмечают точки B , C и D . Из точек A и D как из центров раствором AC описывают две дуги, пересекающиеся в точке E . Расстояние EO равно стороне искомого квадрата. Следовательно, если мы сделаем из A засечки F и G радиусом OE , то A , F , D , G и будут искомыми вершинами квадрата.

256. Если провести 15 прямых так, как показано на рисунке, получится ровно 100 квадратов. У сорока из них сторона равна AB , у двадцати — AC , у восемнадцати — AD , у десяти — AE и у четырех — AF. С помощью 15 прямых можно образовать даже 112 квадратов, но от нас требовалось точно 100. С помощью 14 прямых вам не удастся построить более 91 квадрата.

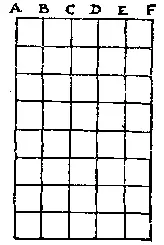
В общем случае с помощью n прямых можно образовать ( n - 3)( n - 1)( n + 1)/24 квадратов, если n нечетно, и ( n - 2) n ( n - 1)/24 квадратов, если n четно.

Если мы имеем m прямых, перпендикулярных другим n прямым, причем m меньше n , то число квадратов равно

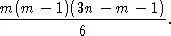
257. Правило заключается в следующем. Если четыре стороны образуют арифметическую прогрессию, то наибольшая площадь равна квадратному корню из произведения всех сторон. Квадратный корень из 70 × 80 × 90 × 100 равен 7099 м 2. Это и есть верный ответ.

258. Площадь дорожки равна точно 66⅔ м 2, что станет совершенно очевидным, если вы представите себе маленький треугольный кусок, отрезанный снизу и перенесенный в правый верхний угол (см. рисунок).

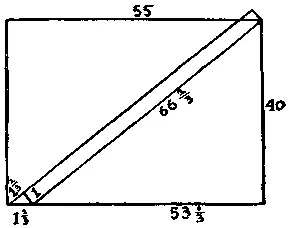
Докажем наше утверждение. Площадь всего сада равна 55 × 40 = 2200 м 2. Но (53⅓ × 40) + 66⅔ также равно 2200. Кроме того, сумма чисел 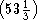2и 40 2должна равняться 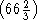2, что и выполняется в действительности.

Общее решение таково. Обозначим ширину прямоугольника через B , длину через L , ширину дорожки через C и длину дорожки через x . Тогда

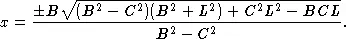
В нашем случае x = 66⅔; следовательно, основание прямоугольного треугольника с гипотенузой 66⅔ м и катетом, равным 40 м, составляет 53⅓ м.

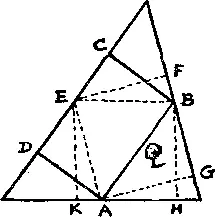
259. Разделим стороны треугольника точками A , B и E пополам. Если провести AB и опустить перпендикуляры DA и CB , то ABCD будет наибольшим возможным прямоугольником, а его площадь составит половину площади треугольника. Два других решения FEAG и KEBH подошли бы нам (у обоих та же самая площадь), если бы они не захватывали дерево. Это правило можно приложить к любому остроугольному треугольнику, а в случае прямоугольного треугольника получатся только два решения.

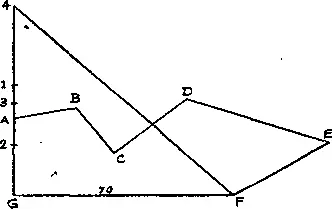
260. Многоугольник с произвольным числом сторон можно свести к равновеликому треугольнику, а поскольку угол AGF оказался прямым, то сделать это очень легко. Продолжим отрезок GA . Приложим линейку к точкам A и C , параллельно перенесем ее вверх до точки B и отметим точку 1. Затем соединим отрезком прямой точки 1 и D и параллельно перенесем его вверх до точки C , отметив точку 2. Теперь приложим линейку к точкам 2 и E , параллельно перенесем ее до точки D и отметим точку 3. Далее соединим линейкой точки 3 и F , параллельно перенесем ее до E , отметив точку 4. Если теперь мы соединим прямой точки 4 и F то получим треугольник G 4 F , площадь которого равна площади нашего неправильного поля. Поскольку на карте GF равно 7 см (70 м), то отрезок G 4 равен 6 см (60 м) и площадь поля равна ½(70 × 60), или 2100 м 2. Этот простой и ценный способ определения площади многоугольников следовало бы знать каждому, но, увы, пока это остается лишь благим пожеланием.