Генри Дьюдени - Пятьсот двадцать головоломок

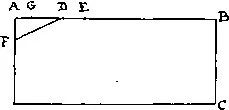
276. Отложим отрезок AD , равный четверти отрезка AB (см. рисунок), и отмерим расстояния DE и AF , каждое из которых составляет ¼ расстояния между точками B и C . Если точка G отстоит от E на то же расстояние, что и точка D от точки F , то длина отрезка AD как раз и будет равна искомой ширине дорожки. Например, если сад имеет размеры 12 × 5 м, то ширина дорожки равна 1 м. Хотя ответ и не всегда выражается целым числом, тем не менее измерения будут верными в любом случае.

277. Правильность приведенного здесь рисунка можно легко проверить, поскольку сумма 15 2+ 20 2= 25 2, сумма 15 2+ 36 2= 39 2и, наконец, 15 2+ 8 2= 17 2, Кроме того, 20 + 8 = 28. Если бы разрешалось брать прямоугольный треугольник, то маленький треугольник слева со сторонами 15, 25, 20 сам мог бы служить решением, так как высота, опущенная на основание (25), равна 12, а медиана 12½.

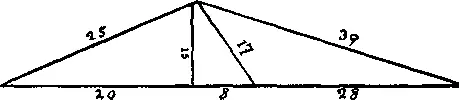
Быть может, наши читатели, пожелав испытать собственные силы, захотят найти общее решение данной задачи?

[Существует и другое решение: тупоугольный треугольник с основанием 66, сторонами 41 и 85 и высотой 40. Медиана этого треугольника равна 58. В этом случае высота опускается на продолжение основания, образуя новый, прямоугольный треугольник с основанием 9 и сторонами 40 и 41. — М. Г. ]

278. Известны лишь расстояния 15 и 6 км. Все, что нужно сделать, — это разделить 15 на 6 и прибавить 2, при этом получится 4½. Разделив затем 15 на 4½) получите 3⅓ км. Это и будет искомым расстоянием между двумя пунктами.

Приведенный способ применим во всех случаях, когда пути образуют прямоугольный треугольник. Простые алгебраические выкладки покажут, откуда взялась константа 2.

Проверить справедливость нашего решения можно следующим образом. Стороны треугольника равны 15, 9⅓ (6 плюс 3⅓) и 17⅔ км (для того чтобы независимо от маршрута расстояние равнялось 21 км). Чтобы избавиться от дробей, умножим все числа на 3 и получим 45, 28 и 53. Если 45 2(2025) плюс 28 2(784) равно 53 2(2809), то все верно, а это равенство можно легко проверить.

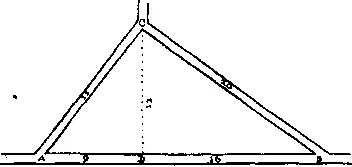
279. На рисунке показаны все расстояния. Спросившему нужно было всего лишь возвести в квадрат 60 км, проделанные первым мотоциклистом (3600), и разделить результат на удвоенную сумму этих 60 и 12 км, составляющих расстояние от дороги AB до C , то есть на 144. Проделав выкладки в уме, он, конечно, заметил, что результат можно получить, разделив 300 на 12, и поэтому сразу же нашел верный ответ — 25 км. Я не показываю здесь, как можно определить, если потребуется, остальные расстояния; сделать это совсем нетрудно.

280. При тех размерах, которые приведены на приложенном к задаче рисунке, никакого треугольника построить вообще нельзя, так как сумма двух меньших сторон не будет превосходить третьей стороны. Очевидно, профессор хотел проверить сообразительность своих учеников.

281. Это снова была шутка. Владелец участка может строить дом, где пожелает, поскольку сумма перпендикуляров, опущенных из любой внутренней точки равностороннего треугольника на стороны, равна высоте данного треугольника.

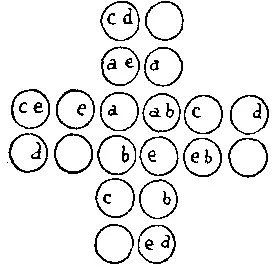
282. Всего таких квадратов 19. Из них 9 того же размера, что и квадрат, отметенный буквами a , 4 того же размера, что и квадрат, отмеченный буквами b , 4 размера c и 2 размера d . Если убрать 6 фишек, отмеченных буквой e , то из оставшихся фишек нельзя будет образовать ни одного квадрата.

[На самом деле квадратов 21. Не сумеет ли читатель найти два квадрата, пропущенные Дьюдени? Ответ на вторую часть задачи остается тем не менее верным. — М. Г. ]

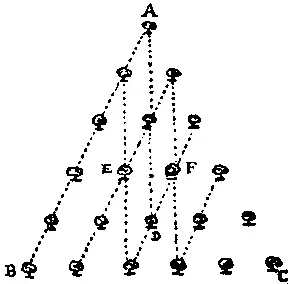
283. Число способов, с помощью которых из 21 дерева можно выбрать 3, равно × × , или 1330. Треугольник можно образовать из любых трех деревьев, не лежащих на одной прямой. Три дерева на пунктирной прямой AB можно выбрать 20 способами, на следующей параллельной прямой с пятью деревьями — десятью способами, на следующей — четырьмя и на следующей — одним способом, что в совокупности составляет 35 способов. Аналогично прямая BC вместе с параллельными даст 35 способов и прямая AC с параллельными — тоже 35 способов. Далее, прямая AD вместе с прямыми, ей параллельными, даст 3 способа, а прямые BF и CE со своими параллельными — по 3 способа каждая. Следовательно, 3 дерева, лежащие на одной прямой, можно выбрать 35 + 35 + 35 + 3 + 3 + 3 = 114 различными способами. Значит, 1330 - 114 = 1216 и есть искомое число способов, с помощью которых можно огородить треугольный участок.

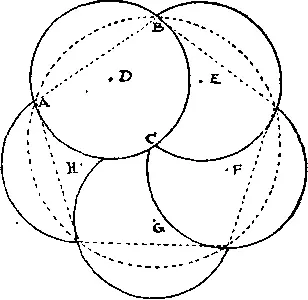
284. На рисунке пунктиром показаны окружность, ограничивающая красный круг, и вписанный в нее правильный пятиугольник. Общий центр окружности и пятиугольника обозначен буквой C . Найдем точку D , равноотстоящую от A , B и C , и радиусом AD проведем окружность ABC . Пять дисков такого размера полностью покроют круг, если их центры поместить в точки D , E , F , G и H . Если диаметр большого круга равен 6 дм, то диаметры дисков немного меньше 4 дм (диаметры дисков равны 4 дм «с точностью до ½ дм»). Если у вас нет никаких тайных отметок на круге, то потребуется немного внимания и тренированности, чтобы класть диски на нужные места, не сдвигая их потом.

Следует добавить, что большой круг можно покрыть, если отношение диаметров превышает 0,6094185, и невозможно, если оно меньше 0,6094180. В нашем случае, когда все диски проходят через центр, отношение равно 0,6180340.

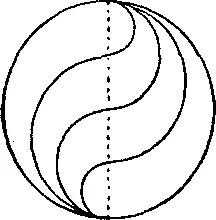
285. Чтобы разделить круглое поле тремя изгородями равной длины на 4 равные части, первоначально следует разделить на 4 части диаметр круга, а затем по обе его стороны описать полуокружности, как показано на рисунке. Изогнутые линии изобразят тогда искомые изгороди.

286. Если построить прямоугольник, у которого одна сторона равна диаметру круга, а другая в 3 раза больше, то его диагональ будет довольно близка к ответу. Практически ее отношение к диаметру будет равно 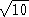, или 3,1622... Мы рекомендуем следующий метод.