Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

6.13.Если меньшее из чисел не оканчивается цифрой 9, то суммы цифр этих чисел различаются на 1. Поэтому обе суммы цифр одновременно делиться на 11 не могут. Нужно искать решение среди чисел, меньшее из которых оканчивается одной или несколькими цифрами 9.

6.14.Нужно правильно использовать условие, в силу которого x и у — целые. Однородное выражение относительно неизвестных нужно оставить слева и попытаться разложить на множители, а число 17 перенести в правую часть равенства.

6.15.Данное уравнение таково, что если x = а , у = b — его решение, то существуют еще три решения: (− а , b ), ( а , − b ), (− а , − b ), если а ≠ b .

6.16.Преобразовать исходное условие к виду 11(4 x − 1) = 69( у − x ) и воспользоваться тем, что x и у — натуральные числа.

7.1.Обе двойки представить как 3 − 1 и сгруппировать члены так, чтобы в числителе можно было вынести за скобки n + 1, а в знаменателе n − 1.

7.2.Прежде чем выполнять действия в скобках, следует упростить дроби, разложив числители и знаменатели на множители.

7.3.Перед нами сумма из трех слагаемых. Если первые два привести к общему знаменателю, то в числителе произойдут существенные упрощения.

7.4.Прежде чем производить вычитание, следует упростить дробь.

7.5.Если вынести за скобки х 2 m , то в скобках останется x в степени, содержащей множителями m − n и 1/ mn . Это упростит дальнейшие преобразования. (!)

7.6.Каждое из подкоренных выражений является полным квадратом.

7.7.Обратить внимание на то, что

9 + 4√2 = 8 + 4√2 + 1 = (2√2 + 1)².

7.8.Каждую из вторых скобок разбить на два слагаемых x ² − u ² и z ² − у ², после чего собрать все члены, содержащие множитель x ² − u ², и все члены, содержащие z ² − у ². (!)

7.9.Если обозначить левую часть через z , то, освобождаясь от радикалов, можно получить уравнение относительно z .

7.10.Равенство, которое нужно доказать, представляет собой однородное выражение седьмой степени. Возвести в степень

а + b + с = 0 и а + b = − с .

7.11.Задача сводится к разбору случаев, позволяющих раскрыть знаки абсолютной величины. Количество рассматриваемых случаев можно уменьшить, если заметить, что равенство, о котором идет речь, не меняется при замене x на − x .

7.12.Можно разобрать различные случаи взаимного расположения чисел x , у и 0. Однако проще возвести каждую часть в квадрат. Так как обе части неотрицательны, то мы получим равенство, равносильное данному. (!)

7.13.Условие можно записать в виде а ⅓+ b ⅓= − с ⅓и возвести это соотношение в куб.

7.14.Данный трехчлен тождественно равен выражению

( ax + b )³ − ( сх + d )³, где а > 0, b > 0, с > 0, d > 0.

8.1.Поскольку выражения, стоящие в скобках, расположены симметрично относительно значения x = 5, удобно ввести новое неизвестное у = x − 5. После того как мы раскроем скобки, произойдут значительные упрощения. (!)

8.2.Можно перемножить скобки по две, чтобы получить квадратные трехчлены, отличающиеся только свободным членом.

8.3.Если записать уравнение в виде x ² − 17 = 3 у ², то возникает мысль доказать, что левая часть ни при каких целых x не делится на 3. (!)

8.4.Если целое у зафиксировать, то получим квадратное уравнение относительно x . Поэтому естественно обратить внимание на те ограничения, которые накладывает на у условие неотрицательности дискриминанта этого уравнения. (!)

8.5.Остаток следует искать в виде аx + b , а частное удобно обозначить через Q ( x ). Следуя определению деления, записать тождество.

8.6.Если переписать уравнение в виде

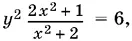
то благодаря условию целочисленности решений можно ограничить возможные значения у рассмотрением нескольких случаев.

8.7.Если подставить известный корень в уравнение, найти коэффициенты при рациональной и иррациональной частях, то получим систему двух уравнений для определения а и b .

8.8.Ответьте на вопрос: достаточно ли воспользоваться теоремой Виета, в силу которой свободный член и второй коэффициент должны быть положительными?

8.9.Если обозначить первый корень через x 1, а знаменатель прогрессии через q , то останется применить теорему Виета. (!)

8.10.С помощью теоремы Виета получить зависимость между α 1, α 2, α 3и коэффициентами данного уравнения. (!)

8.11.Разделить x ³ + аx + 1 на x − α по правилу деления многочлена на двучлен.

8.12.Ясно, что остаток нужно искать в виде аx + b . Если данный многочлен обозначить через P ( x ), а частное от его деления на ( x − 2)( x − 3) — через Q ( x ), то мы сможем воспользоваться определением деления многочленов.

8.13.Если многочлен x 4+ 1 разделится на x ² + рx + q , то в частном мы получим многочлен второй степени, т. е. x ² + аx + b .

8.14.Если данный многочлен делится на ( x − 1)³, то после замены x − 1 = у получим многочлен, который должен делиться на у ³.

8.15.Если многочлен четвертой степени с коэффициентом 6 при старшем члене делится на x ² − x + q без остатка, то в частном обязательно получится многочлен 6 x ² + аx + b , в котором а и b определяются одновременно с p и q .

9.1.Точки −2, −1, 0 делят числовую ось на четыре интервала, в каждом из которых нужно решить данное уравнение. (!)

9.2.Если рассматривать значения x , обращающие в нуль числа, стоящие под знаками абсолютных величин, то придется разбить числовую ось на пять частей.

Удобнее ввести новое неизвестное у = x ². (!)

9.3.Это уравнение четвертой степени. Следовательно, нужно найти искусственный прием, приводящий к его решению. Удобно воспользоваться тем, что слева стоит сумма квадратов.

9.4.Возвести в куб и сравнить полученное уравнение с данным.

9.5.Свести уравнение к симметрической системе, обозначив первое слагаемое левой части через u , а второе через v . (!)

9.6.Если под радикалами раскрыть скобки, то получим квадратные трехчлены, отличающиеся лишь свободным членом. Поэтому данное в условии уравнение удобно заменить системой, обозначив первое слагаемое его левой части через u , а второе через v .