Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

3.14.Достроить усеченную пирамиду до полной и рассмотреть высоты пирамид, имеющих три основания, о которых идет речь в условии.

3.15.Построить угол между скрещивающимися прямыми можно, если параллельно перенести их так, чтобы они проходили через одну точку. В качестве такой точки удобно выбрать вершину А основания пирамиды. Если мы достроим треугольник АВС , лежащий в основании, до параллелограмма АВСЕ (рисунок сделайте самостоятельно), то угол DАЕ будет искомым. Образовавшаяся в результате четырехугольная пирамида будет состоять из ребер данной длины, за исключением ребра DЕ .

3.16.Тетраэдр разбивается на две пирамиды с общим основанием — плоскостью сечения. Данное отношение объемов позволяет найти отношение высот этих пирамид и, следовательно, отношение синусов искомых углов.

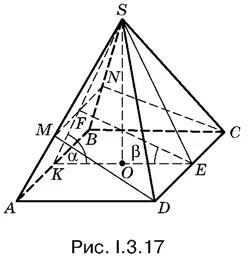
3.17.Условия задачи отражены на рис. I.3.17. Нас интересует отношение площадей треугольников DАМ и DМS , в то время как все известные элементы сосредоточены в плоскости KSЕ . Поэтому нужно связать элементы треугольников DАМ и DМS с элементами треугольника KSЕ .

3.18. Использовать условие задачи, согласно которому высота пирамиды, опущенная из вершины D , проходит через точку пересечения высот основания АВС , с тем, чтобы доказать, что треугольники АDВ и АDС прямоугольные.

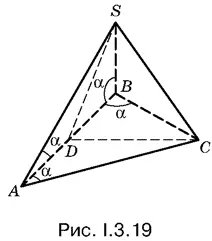
3.19.В пирамиде SАВС (рис. I.3.19) равнобедренные треугольники АSВ и АСВ равны. Следовательно, проведенные в них высоты из вершин S и С упадут в точку D — середину AB .

3.20.Если верхний из двух равных треугольников, лежащих один на другом в плоскости, начать вращать вокруг из общей стороны, то образованный ими двугранный угол может быть как острым, так и тупым. Поэтому придется рассмотреть два случая.

3.21. Если в основании АВС пирамиды провести высоту ВD , то отрезок SD разделит угол АSС пополам.

3.22.Покажите, что отрезки AB и CD взаимно перпендикулярны. Центр описанного шара лежит на их общем перпендикуляре KM , где K — середина СD , M — середина AB .

3.23. Расстояние от основания высоты до бокового ребра измеряется отрезком перпендикуляра, опущенного на боковое ребро. Чтобы связать участвующие в задаче величины, нужно измерить двугранный угол α линейным углом, построенным в точке бокового ребра, которая является основанием этого перпендикуляра. Следовательно, придется построить сечение пирамиды, проходящее через основание высоты и перпендикулярное к боковому ребру пирамиды.

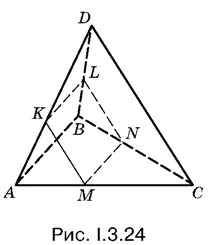
3.24.Чтобы в сечении получился квадрат, плоскость сечения необходимо провести так, чтобы она пересекала все четыре грани пирамиды (иначе мы получили бы в сечении треугольник). Докажите, что если KLNM — квадрат (рис. I.3.24), то плоскость KLNM параллельна двум скрещивающимся прямым AB и СD .

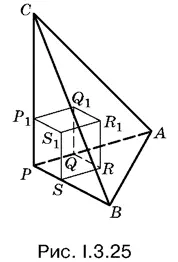
3.25.Для того чтобы найти наиболее рациональное решение задачи, поставьте пирамиду на одну из боковых граней (рис. I.3.25), а затем примените сравнение объемов.

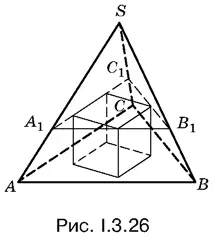
3.26.Вписать в пирамиду куб значит расположить его так, чтобы нижнее основание куба лежало на основании пирамиды, а верхнее основание куба было вписано в треугольник, полученный в горизонтальном сечении пирамиды (рис. I.3.26).

3.27.K решению этой задачи удобно подойти аналитически, рассмотрев общий случай. Предположим, что в сечении образовался некоторый треугольник со сторонами а , b и с . Полезно рассмотреть пирамиду, в основании которой лежит этот треугольник, а вершиной является вершина трехгранного угла.

3.28.По условию задачи попарно равны именно те ребра тетраэдра, которые лежат на скрещивающихся прямых. Использовать это условие можно, если расположить тетраэдр так, чтобы ребро AB лежало в горизонтальной плоскости P , а ребро DС было параллельно этой плоскости.

3.29.Нужно построить расстояние между прямыми AB и CD . Для этого через один из отрезков, например через AB , надо провести плоскость P , параллельную CD .

Решение естественно начать с построения плоскости P , проходящей через одно ребро ( AB ) и параллельной другому ( CD ). Удобный чертеж можно получить, повернув пирамиду вокруг AB так, чтобы плоскость P стала горизонтальной.

Далее нужно построить угол между скрещивающимися прямыми AB и CD . Напомним, что для этого достаточно построить прямую, пересекающую одну из них и параллельную другой.

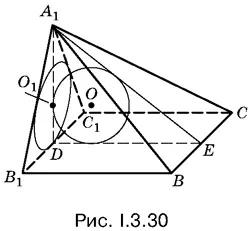
3.30.Плоскость А 1 ВС отсекает от призмы четырехугольную пирамиду. Расположим ее так, как показано на рис. I.3.30. То, что в эту пирамиду вписан шар радиусом R , означает, что в треугольники В 1 А 1 С 1и DА 1 Е вписаны окружности радиусом R .

3.31.В силу соображений симметрии центр шара, о котором идет речь в задаче, совпадает с центром шара, вписанного в правильный тетраэдр.

3.32.Если куб преобразовать подобно, выбрав в качестве центра подобия точку О , то диагональ, проходящая через точку О , сохранит свое направление в пространстве.

3.33.Составным элементом этой задачи является соотношение, связывающее разность углов треугольника, прилегающих к некоторой его стороне, с углом между этой стороной и биссектрисой противоположного угла.

3.34.Диагонали, расстояние между которыми нужно найти, будут лежать на скрещивающихся прямых. Расстояние между скрещивающимися прямыми равно расстоянию между определяемыми ими параллельными плоскостями.

3.35.Так как сфера с центром в точке О расположена симметрично относительно всех трех ребер, выходящих из А , то О должна лежать на диагонали куба.