Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

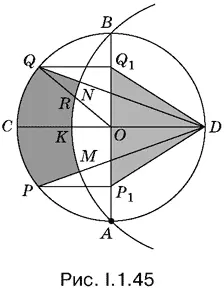
1.46.Соединим точки А и В , P и M и проведем радиусы из центра О в точки А и В (рис. I.1.46). Если длины отрезков AB , АР 1и ОА = R заданы и отрезок AB построен, то прямоугольный треугольник АРВ и положение точки О определяются однозначно. Следовательно, зная длины этих отрезков, можно вычислить длины интересующего нас отрезка РМ .

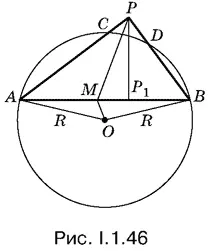
1.47.Отрезок, соединяющий центр окружности с серединой хорды, перпендикулярен к этой хорде. Зная, что хорда удалена от центра на 3 R / 5, легко выразить ее длину через R .

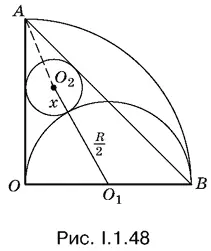
1.48.Использовать геометрически касание окружности О 2с окружностью О 1можно, соединив их центры (рис. I.1.48). Отрезок О 2 О 1пройдет через точку касания. Так как окружность О 2касается сторон угла ОАВ , то ее центр лежит на биссектрисе угла ОАВ .

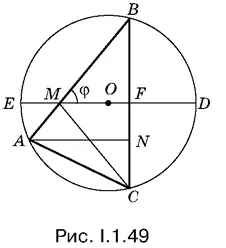
1.49.Если в треугольнике АВС провести высоту АN (рис. I.1.49), то искомая площадь будет равна ½ АN · BC . Соединив точки M и С , разобьем треугольник АВС на равнобедренный треугольник МСВ и треугольник АМС , у которого угол АМС легко выразить через φ.

1.50.Задача вычислительная. Нужно воспользоваться формулой Герона и выражением радиуса R через стороны треугольника и его площадь S , т. е. R = abc / 4 S . Стороны треугольника удобно обозначить: а , а − d , а + d .

1.51.Проведите через точки P и Q прямые, параллельные AC . Первая будет средней линией треугольника АВС , вторая — средней линией треугольника с вершиной В , которому первая средняя линия служит основанием.

1.52.Соединим точки P и T . Данный треугольник разбивается на пять. Пусть QT = m , TL = n , QN = RL = а . Чтобы использовать условия задачи, можно записать соотношения площадей различных треугольников, образовавшихся из данного треугольника PQR .

1.53.Хорда MN — сторона правильного шестиугольника, вписанного в первую окружность, так как опирающийся на MN центральный угол ∠ МО 1 N = 60°. Чем является MN для второй окружности?

1.54.Для вписанного в окружность четырехугольника воспользоваться свойством, в силу которого сумма противоположных его углов равна 180°. Удобно обозначить стороны четырехугольника через а , b , с , d , начиная со стороны AB , а опирающиеся на них углы (проведите диагонали) через α, β, γ, δ.

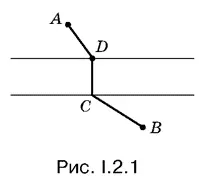
2.1.Предположим, что где-то построен мост (рис. I.2.1). В этом случае путь из А в В будет ломаной, состоящей из трех звеньев. Среднее звено всегда остается неизвестным по длине и направлению. Следовательно, нужно «спрямить» первое и третье звенья.

2.2.Из точки А отрезки МР и РN видны под углом 30° каждый. Следовательно, построить точку А можно как пересечение двух сегментов, вмещающих угол в 30°.

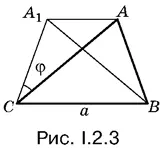
2.3.Пусть треугольник АВС искомый (рис. I.2.3). Чтобы на чертеже появился угол φ, отразим треугольник АВС от вертикальной оси, проходящей через середину BC . Получим треугольник СА 1 А , в котором ∠ А 1 СА = φ.

2.4.В любом треугольнике АВС центр описанной окружности лежит на пересечении перпендикуляров, восставленных из середин сторон. Этот факт можно использовать для того, чтобы связать данные элементы треугольника: b и m с .

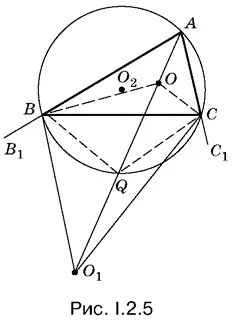
2.5.Точки О (центр вписанной окружности) и О 1(центр вневписанной окружности) лежат на биссектрисе угла А треугольника АВС (рис. I.2.5). Отрезки ОС и О 1 С , ОВ и О 1 В взаимно перпендикулярны как биссектрисы смежных углов. Поэтому точки В , О , С , О 1лежат на одной окружности с центром в точке Q .

2.6.Применить метод подобия, выбрав за центр подобия одну из вершин треугольника, А или С .

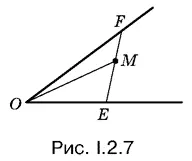
2.7.Если прямую FЕ (рис. I.2.7) вращать около точки M , то площади треугольников ОМF и ОМЕ будут изменяться так, что с увеличением одной уменьшается другая. Это должно навести на мысль рассмотреть некоторое среднее положение.

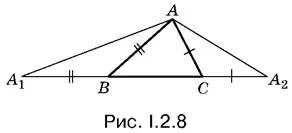
2.8.Чтобы использовать данный в условии периметр треугольника, нужно осуществить «спрямление», т. е. рассмотреть треугольник, который получается из искомого, если отложить на BC отрезки А 1 В и СА 2, равные AB и AC соответственно, так, как это показано на рис. I.2.8.

2.9.Чтобы подойти к решению задачи, нужно построить из отрезков АР , ВР и СР ломаную с закрепленными концами и посмотреть, когда эта ломаная будет выпрямляться.

2.10.Зная гипотенузу, можно построить окружность, в которую вписан искомый прямоугольный треугольник АВС . Если биссектрису CD продолжить до пересечения с этой окружностью в точке E , то получим две равные дуги АЕ и ЕВ . Следовательно, отрезок ОЕ , соединяющий точку E с центром круга, перпендикулярен к AB и равен c / 2. Теперь все данные в условии элементы связаны между собой.

2.11.Пусть известны углы при вершинах А и D четырехугольника и его стороны AB = а , BC = b , CD = с . Если угол ВАD закреплен, то положение точки С определяется с помощью метода геометрических мест.

2.12.Пусть AM (рис. I.2.12) — искомая секущая и AB = ВМ . Чтобы связать ее с данной окружностью, соединим точки О и В . Если отрезок ОВ продолжим за точку В и отложим BC = ОВ = R , то точки О , А , С и M будут вершинами параллелограмма.