Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
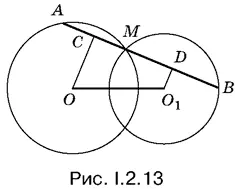
2.13.Пусть через точку M пересечения двух окружностей с центрами О и О 1(рис. I.2.13) проведена секущая AB данной длины. Проведем к ней перпендикуляры ОС и О 1 D . Отрезок CD вдвое меньше отрезка AB , так как точки С и D — соответственно середины хорд AM и МВ .
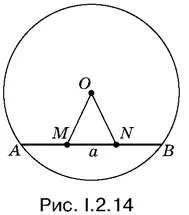
2.14.Если хорда AB искомая, то МВ − AM = а . Построим отрезок BN , равный AM (рис. I.2.14). Точки M и N лежат на одинаковом расстоянии от точки О , а MN = а .
2.15.Так как длина отрезка PQ и несущая его прямая известны, то можно воспользоваться методом параллельного переноса.
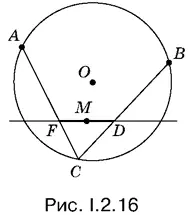
2.16.Нужно построить отрезок FD (рис. I.2.16), делящийся в точке M пополам. Следовательно, его можно рассматривать как одну из диагоналей параллелограмма. В качестве одной из вершин параллелограмма удобно выбрать точку В . Отразив ее симметрично от точки M , получим еще одну вершину.
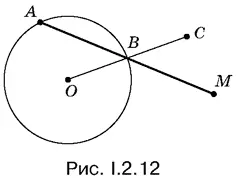
2.17.Если через точки А и В провести прямую, то она, вообще говоря, должна пересечь прямую PQ в некоторой точке С . Остается воспользоваться свойством секущей и касательной, проходящих через общую точку. Случай, когда AB и PQ параллельны, рассмотрите отдельно. (!)
2.18.Соединить точку M с концами А и В данного диаметра. Рассмотреть получившиеся точки пересечения с окружностью.
2.19.Воспользоваться предыдущей задачей и построить произвольный перпендикуляр к данному диаметру, пересекающий окружность в точках С и D .
2.20.Какую бы точку С на прямой l мы ни взяли, величина | AC − BC | в силу неравенства треугольника не может превзойти длины отрезка AB . Следовательно, существует точка прямой l , отвечающая требованиям задачи. По условию точки А и В лежат по разные стороны прямой l . Принципиально ли это требование, или же можно сформулировать эквивалентную задачу для точек, лежащих по одну сторону прямой l ?
2.21.Для построения естественно воспользоваться обычным методом геометрических мест. Каждая вершина квадрата лежит на внешней половине окружности, построенной на стороне четырехугольника как на диаметре. Чтобы отыскать второе геометрическое место точек, которому принадлежат вершины, нужно выяснить, что связана какая-то из линий, определяющих вершины, с данным четырехугольником. Рассмотрите с этой целью диагональ квадрата.
2.22.Дан отрезок и известно, что его длина 7. Отрезок длины 1 не известен. Если бы он был дан, то отрезок длины √7 можно построить, как только мы построим отрезок длины √3. Затем построим гипотенузу прямоугольного треугольника со сторонами √3 и 2.
2.23.Решение можно искать только при одновременном выполнении условий:
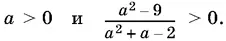
K главе 3
3.1.Чтобы связать участвующие в задаче элементы, нужно отрезок ОА луча, перпендикулярного к ребру, спроецировать на другую полуплоскость. Проекцию ОВ этого отрезка спроецировать в отрезок ОС , лежащий на втором луче.
3.2.Чтобы связать данные углы с величиной угла, который нужно найти, следует спроецировать катеты треугольника на плоскость P и построить искомый угол.
3.3.При проецировании угла α на плоскость P возникает четырехгранный угол, в котором три плоских угла даны, а два двугранных угла прямые. Чтобы установить связь между плоскими углами, нужно пересечь этот четырехгранный угол плоскостью Q , перпендикулярной к плоскости P .
3.4.Если спроецировать искомую прямую, параллельную а , на плоскость, перпендикулярную к а , то мы получим точку. Спроецируйте на эту же плоскость три оставшиеся прямые.
3.5.Начать нужно с построения искомого угла. Для этого прямые AB и SC нужно перенести в одну точку. Если сместить прямую SC , то она «повиснет в воздухе» и угол, который мы получим, не будет связан с треугольником. Поэтому проведем через току C прямую CD , параллельную AB ; угол SCD искомый.
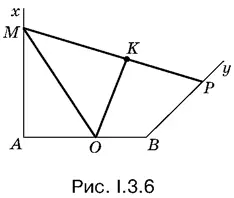
3.6.Лучи Аx и Вy удобно расположить так, как показано на рис. I.3.6. Утверждение, что ОК = АО , равносильно утверждению, что АM = MK (рассмотрите прямоугольные треугольники ОАМ и OKM ).
3.7.Если такое сечение четырехгранного угла существует, то в результате параллельного сдвига плоскости этого сечения мы получим новую плоскость, пересечение которой с четырехгранным углом — тоже параллелограмм. Поэтому строить сечение можно в любой точке ребра четырехгранного угла.
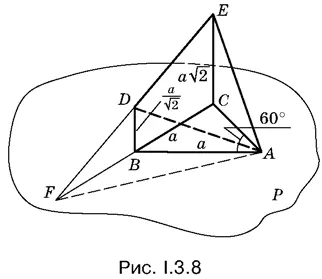
3.8.Если продолжить DE и BC до пересечения в точке F , то BD — средняя линия в треугольнике EFC (рис. I.3.8). Площадь треугольника DEА равна половине площади треугольника FEA .
3.9.Чтобы ответить на вопрос задачи, нужно определить высоту H пирамиды. Каждый из данных двугранных углов можно измерить с помощью линейного угла, опирающегося на высоту H . Остается использовать тот факт, что в основании лежит правильный треугольник.
3.10.Докажите, что высота, проведенная в треугольнике АDВ через вершину D , проходит через середину E основания AB . Тогда интересующий нас двугранный угол измеряется линейным углом DEC .
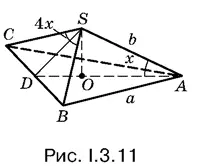
3.11.Условия задачи отражены на рис. I.3.11. Сторона а основания известна, так как известна площадь основания.
3.12.Аналогичное построение на плоскости приводит к образованию треугольника, подобного данному, с коэффициентом подобия ½. Поэтому и здесь следует постараться выяснить, подобны ли рассматриваемые тетраэдры.
3.13.Если О — центр шара, касающегося боковых граней пирамиды в точках О 1, О 2и О 3(рис. I.3.13), то легко установить, что SB 1= SB 2= SB 3. Если мы сумеем доказать равенство треугольников А 2 SВ 1и А 2 SВ 3, то установим, что в основании пирамиды лежит правильный треугольник.
Читать дальшеИнтервал:
Закладка:










