Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

1.18.Воспользоваться методом сравнения площадей.

1.19.Точки A , О и L лежат на одной прямой — биссектрисе угла ВАС , аналогично точки В , О и K лежат на биссектрисе угла АВС . Прямая KL делит угол АСМ пополам ( СМ — продолжение BC ).

По условию A = 2 С , а В = 4 С (рисунок сделайте самостоятельно).

1.20.Так как сумма углов в треугольнике равна π, то углы А , В и С нетрудно вычислить.

1.21.Сделать несложное дополнительное построение, чтобы получились подобные треугольники.

1.22.Поскольку отрезки, длины которых входят в правую часть равенства, лежат на одной прямой, нужно выразить длины всех отрезков на той же прямой. Тем самым мы «спрямим» записанное соотношение и сделаем его доказательство простым.

1.23.В формулу входят отношения. Поэтому целесообразно сделать дополнительные построения, в результате которых получатся подобные треугольники.

1.24.При построении, описанном в условии, возникают подобные треугольники. Нужно с их помощью заменить стоящие в левой части отношения новыми отношениями с тем, чтобы в знаменателе была одна и та же сторона треугольника, а в числителе — отрезки этой стороны. (!)

1.25.Положение прямой, проходящей через точку О , можно определить с помощью угла α, который эта прямая составляет с некоторым фиксированным радиусом описанной окружности. Нужно доказать, что величина, о которой говорится в условии, не зависит от α.

1.26.Чтобы ответить на вопрос задачи, нужно знать стороны данного треугольника и радиус описанной около него окружности. С вычисления этих величин и следует начать решение задачи.

1.27.Связать углы треугольника и его стороны можно либо с помощью теоремы синусов, либо с помощью теоремы косинусов. Данное в условии соотношение между сторонами треугольника подсказывает, что теорема косинусов удобнее.

1.28.Если отрезки ОА , ОВ и ОС , входящие в данное соотношение ОА ² = ОВ · ОС , выразить через радиус r вписанной окружности и углы треугольника, то должно получиться соотношение между тригонометрическими функциями этих углов, не содержащее r . (!)

1.29.Применить формулу, выражающую площадь треугольника через две стороны и синус угла, и теорему косинусов. (!)

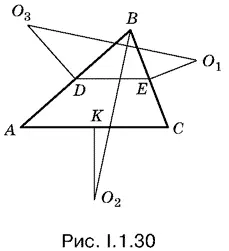
1.30.Чтобы доказать равенство двух отрезков, о которых идет речь в условии, можно ввести элементы, определяющие треугольник, и выразить через них эти отрезки. То же самое можно сделать геометрически: четырехугольник О 1 ЕDО 3(рис. I.1.30), построенный на отрезке О 1 О 3, таков, что каждая из трех его остальных сторон равна половине соответствующей стороны треугольника. Остается построить такой же четырехугольник на отрезке ВО 2.

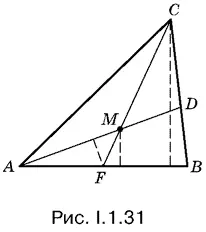
1.31.Площадь треугольника АFМ (рис. I.1.31) в восемь раз меньше площади треугольника АВС, так как АF = ½ AB , а высота треугольника АFМ в четыре раза меньше высоты треугольника АВС (докажите). Если рассматривать AM и АD как основания треугольников АFМ и АВD , то соответствующие высоты этих треугольников относятся как 1 : 2. Выяснив, в каком отношении точка M делит отрезок АD , мы решим задачу.

1.32.Так как четырехугольник вписанный, то кроме входящих в задачу величин целесообразно рассмотреть радиус круга R и углы четырехугольника. Введя углы, мы сможем использовать свойство вписанного четырехугольника.

1.33.Использовать тот факт, что боковые стороны трапеции и отрезок, соединяющий середины ее оснований, лежат на прямых, пересекающихся в общей точке.

1.34.Если обозначить сторону квадрата через а, а расстояние от точки M до самой ближней стороны (либо до AB , либо до CD ) через x , то остальные расстояния можно выразить через а и x .

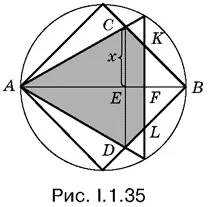
1.35.Фигура, площадь которой нужно определить, на рис. I.1.35 заштрихована. Отрезок CD разбивает эту фигуру на правильный треугольник и трапецию. Длина отрезка АF известна, она равна 3/ 2. Если мы сможем определить длину отрезка СЕ (обозначим ее x ), то задача будет решена.

1.36.Из параллельности сторон трапеции и треугольника следует, что углы при основании треугольника и при нижнем основании трапеции равны. Если обозначить эти углы через α, то можно выразить через α и другие углы, связанные с треугольником и трапецией.

1.37.Треугольники АОD и BОС подобны. Это позволяет из отношения оснований трапеции получить отношение высот треугольника АОD и трапеции. (!)

1.38.Нас интересует периметр третьего многоугольника. Обозначим его через x . Введем также радиус окружности R и число сторон b первого многоугольника.

1.39.Окружность не может лежать между точками M и О (докажите). Ее центр О 1лежит на биссектрисе угла АОВ .

1.40.Из данного отношения площадей треугольников АВС и АDЕ , записанного в виде отношения произведений катетов, и из свойства произведения секущей на ее внешнюю часть найти отношение AE / AB .

1.41.Пусть О 1— центр окружности, радиус которой мы ищем, а О — центр данной окружности. В качестве связующего звена следует рассмотреть треугольник АОО 1.

1.42.Нужно обозначить сторону квадрата через а и составить с помощью теоремы Пифагора биквадратное уравнение для определения а через R и r .

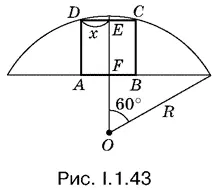
1.43.Вписанный в сегмент квадрат не должен нарушать симметрии сегмента. Поэтому он расположится так, как показано на рис. I.1.43. Обозначим половину стороны квадрата через x и составим уравнение относительно x .

1.44.Чтобы использовать условия задачи, нужно провести радиусы обеих окружностей в точки касания окружностей друг с другом и с нижним основанием. Центр меньшей окружности лежит на биссектрисе угла D .

1.45.Вначале для определенности удобно предположить, что точки P и Q лежат по разные стороны от CD . В этом случае диаметр CD разделит фигуры РQNМ и Р 1 Q 1 D на две части (рис. I.1.45). Нужно доказать, что площадь фигуры СQNK равна площади треугольника Q 1 OD . При этом полезен будет следующий факт. Если соединить точки Q и О , то, во-первых, угол QОС вдвое больше угла QDС , а во-вторых, треугольники ОQ 1 D и ОQD равновелики.