Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Соединения и бином

Эта глава содержит задачи по комбинаторике, а также задачи, связанные с возведением в степень двучлена ax + b . Выражение ( ax + b ) называют биномом Ньютона и рассматривают, как правило, его разложение в ряд по степеням x и коэффициенты этого разложения — они зависят от а и b — при различных степенях x .

Комбинаторика изучает всевозможные комбинации из элементов данного конечного множества. Простейшие из таких комбинаций: перестановки, размещения и сочетания.

Перестановки состоят из одних и тех же элементов некоторого множества и отличаются одна от другой только порядком их расположения. Число всех возможных перестановок для множества, состоящего из n различных элементов, обозначают P ( n ):

P ( n ) = 1 · 2 · 3 · ... · n = n ! (1)

Символ n ! (читается «эн факториал») обозначает произведение первых n чисел натурального ряда: 1! = 1, 2! = 2, 3! = 6, 4! = 24, ... . По определению 0! = 1.

Следующий вид комбинаций — размещения из n различных элементов, образующих множество, в группы по k различных элементов в каждой. При этом два размещения считают разными, если они отличаются либо элементами, либо порядком их расположения. Подобные ситуации возникают при размещении постояльцев в гостинице, зрителей в театральном зале, пассажиров в поезде. Число всех возможных размещений по k различных элементов в каждом размещении, формируемых из n различных элементов данного множества, обозначают А n k . Имеет место формула:

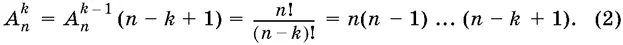
Сочетания из n элементов по k элементов — комбинации, составленные из данных n элементов и содержащие по k ( k ≤ n ) элементов в каждой, отличающиеся одна от другой хотя бы одним элементом. С — число сочетаний из n по k :

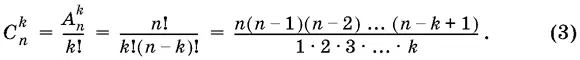
Наряду с соединениями, в которые каждый из n различных элементов некоторого фиксированного множества входит один раз, можно рассматривать соединения с повторениями, допускающие появление одного и того же элемента более одного раза.

Если задан алфавит из n различных букв и поставлена задача составить всевозможные слова по k букв в каждом, то речь идет о размещениях с повторениями. Обратите внимание на то обстоятельство, что слова могут быть любой длины, а потому нет необходимости в выполнении ограничения k ≤ n . Слова aba и baa считаются различными (входящие в них элементы образуют разные последовательности).

Число 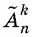всевозможных различных размещений с повторениями из n различных элементов по k элементов в каждом находится по формуле

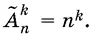
Доказывается эта формула с помощью рекуррентного соотношения

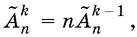
которое устанавливается следующим рассуждением. Если первая буква в слове из k букв фиксирована, то в оставшиеся k − 1 ячеек можно разметить буквы 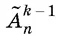способами. Для каждого из этих способов остается n возможностей для выбора буквы, стоящей на первом месте. В результате мы получим все размещения с повторениями из n по k .

Размещения с повторениями, образованные из n элементов a 1, a 2, ..., а n так, что каждый из этих элементов входит в размещение по крайней мере один раз, называются перестановками с повторениями. Если известно, что элемент a 1входит α 1раз, элемент a 2входит α 2раз, ..., элемент a n входит α n раз, то число всевозможных таких перестановок обозначают 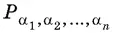и оно может быть найдено по формуле

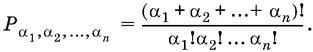
Два сочетания с повторениями из n элементов по k в каждом считаются различными тогда и только тогда, когда они отличаются по крайней мере одним элементом или какой-нибудь элемент входит в эти соединения различное число раз. Число всевозможных сочетаний с повторениями определяется по формуле

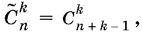
вывод которой состоит в доказательстве того факта, что допущение о возможности повторений элементов равносильно увеличению числа элементов, из которых образуются сочетания, на k − 1.

Для любого натурального n справедливы разложения

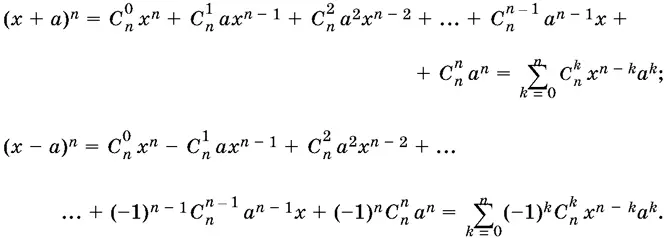
Для биномиальных коэффициентов справедливы равенства:

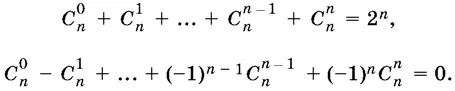
21.1.Сколькими различными способами можно усадить за круглый стол n человек, если два способа считаются одинаковыми, когда каждый человек имеет тех же соседей (левый и правый соседи не различаются).

21.2.Имеется одна перестановка из пяти элементов: а 1, а 2, а 3, а 4, а 5. Найдите число всех перестановок из этих элементов, в каждой из которых на первом месте стоит элемент, отличный от а 1, а на втором — элемент, отличный от а 2.

21.3.Сколько можно образовать семизначных чисел из цифр 1, 2, 3, ..., 8 с тем, чтобы цифра 2 входила в каждое число не меньше, чем три раза?

21.4.Сколько восьмизначных чисел можно образовать из цифр 0, 1, 2, 3, 4, 5, если в каждом числе цифра 1 содержится три раза, а остальные цифры по одному разу?

21.5.Экскурсанты заказали на пароходе 8 четырехместных кают. Все места в каждой из кают и все каюты равноценны. Сколькими способами могут экскурсанты разместиться в каютах, если их 32 человека?

21.6.Вычислите сумму

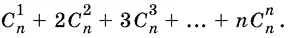
21.7.Найдите все значения n , при которых какие-либо три последовательных коэффициента разложения бинома ( x + а ) n являются тремя последовательными членами арифметической прогрессии.