Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

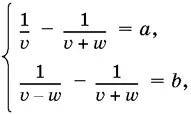
которую не пришлось бы преобразовывать.

Разберем еще одну задачу, на примере которой видно, как решаются задачи на движение.

Пример 3.Из пункта С в пункт D выехал товарный поезд. Через 5 ч 5 мин навстречу ему из пункта D выехал пассажирский поезд. Они встретились в каком-то пункте А . После этого пассажирский поезд приехал в пункт С через 4 ч 6 мин, а товарный — в пункт D через 12 ч 55 мин. Сколько времени каждый поезд находился в пути?

Условия задачи можно отразить на схеме (рис. 18.1), где буквой В обозначено положение товарного поезда в момент выхода пассажирского из пункта D .

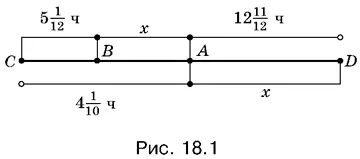
То обстоятельство, что оба поезда находились в точке А одновременно, мы отразим на схеме с помощью вертикального отрезка, связывающего оба пути. Схема подсказывает нам и выбор неизвестных. На путь от В до А товарный поезд потратил столько же времени, сколько пассажирский на путь от пункта D до А . Если обозначить это время через x, то на схеме не останется «белых пятен».

Пусть v 1— скорость товарного поезда, а v 2— скорость пассажирского поезда. Каждый из отрезков пути: от пункта С до А и от пункта D до А позволяет составить уравнения

12 11/ 12 v 1= хv 2, (5 1/ 12+ x ) v 1= 4 1/ 10 v 2.

Можно составить и уравнение для всего пути:

(5 1/ 12+ x + 12 11/ 12) v 1, = ( x + 4 1/ 10) v 2,

которое является следствием (точнее, суммой) первых двух уравнений. Однако это уравнение проще второго. Поэтому мы будем решать систему

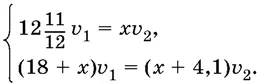
Разделив первое уравнение на второе, получим

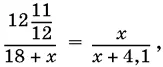
откуда x = 5 ч 10 мин (второй корень отрицательный и не имеет физического смысла). Итак, товарный поезд пройдет весь путь за 23 ч 10 мин, а пассажирский — за 9 ч 16 мин.

18.1.Бассейн наполняется четырьмя трубами за 4 ч. Первая, вторая и четвертая заполняют бассейн за 6 ч. Вторая, третья и четвертая — за 5 ч. За сколько времени заполняют бассейн первая и третья трубы?

18.2.У продавца испортились весы (плечи весов оказались неравными). Продавец отпустил покупателю два веса: первый раз на одну чашку весов положил килограммовую гирю, а на вторую — товар, во второй раз поменял гирю и товар местами. Компенсировал ли продавец неточность весов?

18.3.Школьник переклеивает свои марки в новый альбом. Если он наклеит по 20 марок на один лист, то ему не хватит альбома, если по 23 марки, то по крайней мере один лист останется пустым. Если школьнику подарить еще один такой же альбом, на каждом листе которого наклеено по 21 марке, то всего у него станет 500 марок. Сколько листов в альбоме?

18.4.Одному буксиру нужно перевезти за наименьшее время два понтона вниз по реке на l км. Было решено, что один понтон будет отправлен по течению реки самостоятельно, а другой будет некоторое время транспортироваться буксиром, после чего буксир оставит его и вернется за первым и отбуксирует его до конечного пункта. Сколько километров должен транспортироваться второй понтон, чтобы оба пришли к конечному пункту одновременно, и сколько потребуется времени на всю перевозку, если собственная скорость буксира v км/ч, а скорость течения реки u км/ч?

18.5.Некто родился в девятнадцатом веке (до 1900 года). В 1901 году сумма цифр числа, выражающего год его рождения, равнялась сумме цифр числа, выражающего количество прожитых лет. Определите, в каком году родился некто.

18.6.Цена бриллианта пропорциональна квадрату его массы. Бриллиант массой p карат был разбит на две части, после чего его стоимость уменьшилась в k раз. Найдите массы частей, на которые был разбит бриллиант [12] 1 карат = 0,2 г. .

18.7.Некоторую часть маршрута туристам предстоит совершить вверх по реке. В их распоряжении моторная лодка, способная развивать две скорости с разным расходом горючего. Если скорость течения реки окажется равной u км/ч, то при движении на любой из собственных скоростей будет затрачено одинаковое количество горючего. Если же скорость течения в k раз больше ( k > 1), то при движении с собственной скоростью v 1горючее будет израсходовано полностью, а при движении с собственной скоростью v 2останется A кг горючего. Какое количество горючего будет затрачено на весь путь?

18.8.У продавца мороженого есть по нескольку десятков порций мороженого пяти сортов — за 7, 9, 11, 13 и 15 p. Общее число порций равно 180, а общая стоимость — 1840 p. Порций мороженого по 7 и 9 p. вместе столько же, сколько по 11, 13 и 15 p. вместе. Кроме того, известно, что порций по 9 p. вдвое больше, чем по 15 p., и больше, чем по 13 p. Определите число порций каждого сорта.

18.9.Плоты шли из пункта A до устья реки вниз по течению. У устья реки их взял на буксир пароход и через 11,5 суток после выхода плотов из пункта A доставил их по озеру в пункт B . Сколько времени пароход вел плоты от устья реки по озеру до B , если известно, что пароход совершает рейс (без буксировки) от A до B за 40 ч и от B до A за 48 ч, а скорость во время буксировки уменьшается вдвое.

18.10.Три пловца должны проплыть из A в B и обратно. Сначала стартует первый, через 5 с — второй, еще через 5 с — третий. Некоторую точку C , находящуюся между пунктами A и B , все пловцы миновали одновременно (до этого времени ни один из них в B не побывал). Третий пловец, доплыв до B и повернув назад, встречает второго в 9 м от B , а первого — в 15 м от B . Найдите скорость третьего пловца, если расстояние AB равно 55 м.

18.11.Сосуд, содержащий p %−й раствор кислоты, долили доверху q %−м раствором кислоты и после перемешивания отлили то же количество. Проделав эту операцию k раз, получили r %−й раствор. Какую часть объема сосуда занимал первоначальный раствор [13] Плотности всех растворов предполагаются одинаковыми; при сливании двух растворов объем нового раствора равен сумме объемов исходных растворов. ?

18.12.Из пункта A в пункт B выехал автомобиль. Одновременно из B навстречу ему выехал мотоцикл. Через некоторое время они встретились. В момент их встречи из B в A выехал второй мотоцикл и в некоторый момент времени встретился с автомобилем. Расстояние между пунктами первой и второй встреч равно 2/ 9 AB . Если бы скорость автомобиля была на 20 км/ч меньше, то автомобиль встретился бы с первым мотоциклом через 3 ч после их выезда и расстояние между пунктами встреч было бы равно 60 км. Найдите AB , если скорости обоих мотоциклов одинаковы.