Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

t 1 x = t 2 у = t 3 z = ⅓. (1)

Мы получили три уравнения (их можно было написать в виде t 1 x = ⅓, t 2 у = ⅓, t 3 z = ⅓. K ним нередко добавляют четвертое:

t 1 x + t 2 у + t 2 z = 1,

которое должно отражать то обстоятельство, что в итоге вся работа была выполнена. Однако это уравнение не содержит никакой самостоятельной информации: оно является следствием первых трех и получается в результате их сложения. Поэтому последнее уравнение, хотя и верно составлено, но бесполезно для решения задачи.

Так как первый и второй рабочие вместе выполняют всю работу за 1/ x + y ч, а третьему на это потребуется 1/ z ч, то еще одно условие задачи можно записать так:

1/ x + y + 9 = 1/ z . (2)

Составим теперь уравнение, отражающее тот факт, что третий рабочий приступил к работе, когда ее 1/ 6была выполнена. Другими словами, когда первый проработал t 1− t 3ч, а второй t 2− t 3ч, они сделали 1/ 6всей работы:

x ( t 1− t 3) + у ( t 2− t 3) = 1/ 6. (3)

Добавляя к этим пяти уравнениям шестое:

t 2− t 3= 2, (4)

мы можем приступить к решению полученной системы уравнений.

Решая систему уравнений, как правило, следует держать в поле зрения два обстоятельства. Во-первых, систему уравнений нужно воспринимать в целом, так, как вы воспринимали бы ее, решая вне связи с задачей. Это позволит найти более рациональный ключ к ее решению. Во-вторых, нельзя упустить из виду те неизвестные (или комбинации неизвестных), которые позволят ответить на вопрос задачи. Благодаря этому можно обойтись без излишних вычислений.

В нашем примере второе обстоятельство должно побудить нас использовать уравнение (4) для упрощения уравнения (3), в результате чего из (3) будет исключено неизвестное t 2, которое нас не интересует. Однако после замены t 2− t 3на 2 уравнение (3) потеряет симметрию относительно t 1 x и t 2 у , что затруднит использование уравнений (1). Если же в уравнении (3) раскрыть скобки и вспомнить, что xt 1= ⅓ и уt 2= ⅓, то получим уравнение

t 3( x + у ) = ½.

С его помощью можно выразить x + у через t 3, а из уравнения zt 3= ⅓ можно выразить через t 3и неизвестное z . Подставляя эти выражения в (2), получим

2 t 3+ 9 = 3 t 3,

откуда

t 3= 9.

Дальнейшее решение системы не представляет труда. Находим последовательно: t 2= 11, z = 1/ 27, у = 1/ 33. Из уравнения (2) определяем x = 5/ 198и t 1= 1/ 3 x = 66/ 5. Итак, первый рабочий работал 13 ч 12 мин.

Эту же задачу можно было бы решить с помощью меньшего числа неизвестных, если ввести в рассмотрение, помимо величин x , у и z , имеющих прежний смысл, величину t , обозначающую время, в течение которого рабочие работали вместе, т. е. время работы третьего рабочего. Это привело бы нас к системе:

t ( x + у + z ) = 5/ 6 (1′)

(за время t рабочие сделали вместе 5/ 6 всей работы),

tz = ( t + 2) у = ⅓ (2′)

(за время t третий рабочий сделал треть всей работы, а второму на это потребовалось на 2 ч больше),

1/ x + y + 9 = 1/ z (3′)

(первый и второй рабочие выполняют всю работу на 9 ч быстрее, чем третий, работая один).

Поскольку tz = ⅓, то из (1′) найдем

x + y = 1/ 2 t .

Вместе с z = 1/ 3 t подставим в (3′). Получим

t = 9.

Как и прежде, найдем последовательно z, у и x . На вопрос задачи можно ответить, вспомнив, что первый рабочий работал столько, чтобы успеть сделать ⅓ всей работы, т. е. 1/ 3 x .

Конечно, второе решение выглядит более изящно, чем первое. Однако признать его лучшим трудно, поскольку за те простые уравнения, от которых мы отказались, пришлось уплатить некоторым усложнением логики.

А теперь приведем арифметическое решение этой задачи — решение, в котором удается обойтись вообще без составления уравнений.

Так как рабочие совместно выполнили 1 − 1/ 6= 5/ 6всей работы, причем третий сделал ⅓, то на долю первого и второго осталось 5/ 6− ⅓ = ½ всей работы. Следовательно, если бы первый и второй успели выполнить всю работу, то третий за то же самое время сделал бы ⅔; ему останется 1 − ⅔ = ⅓ , на что ему потребовалось бы в силу последнего условия задачи 9 ч.

Так как каждый рабочий сделал одинаковое количество деталей, т. е. ⅓ всей работы, то третий работал ровно 9 ч. Тогда второй работал 9 + 2 = 11 ч. Так как он тоже сделал ⅓ всей работы, то его производительность равна 1/ 33всей работы в час. Мы знаем, что первый и второй тратят на ½ всей работы столько же, сколько третий на ⅓, т. е. 9 ч. Второй сделает за это время 33 · 9 = 3/ 11всей работы. Следовательно, на долю первого приходится ½ − 3/ 11= 5/ 22. Его производительность 5/ 22: 9 = 5/ 198в час. Свою треть работы он выполнил за ⅓ : 5/ 198= 13 1/ 5 (ч), т. е. за 13 ч 12 мин.

Хотя решение выглядит намного красивее, чем первые два, его тоже трудно назвать существенно лучшим. Взгляните внимательно на уравнения второго решения, и вы заметите, что третье решение получено почти «дословным» пересказом этих уравнений.

Таким образом, на пути к решению задачи вас не должно останавливать большое число неизвестных, которые, по вашему мнению, следует ввести.

Однако старайтесь не вводить неизвестные, размерность которых не встречается в условии и не может быть получена как комбинация элементов условия. Введение таких неизвестных может усложнить задачу.

Вот простой пример.

Пример 2.Расстояние между двумя пунктами A и В пароход проходит по течению реки на а ч быстрее, чем то же расстояние в стоячей воде, и на b ч быстрее, чем против течения ( b > а > 0). За какое время пароход проходит расстояние от A до В по течению?

Если ввести в рассмотрение неизвестные: v — скорость парохода в стоячей воде, w — скорость течения реки, x — расстояние, то получим систему двух уравнений с тремя неизвестными:

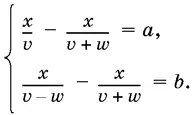
Найти из этой системы величину x / v + w можно, если сделать следующие преобразования:

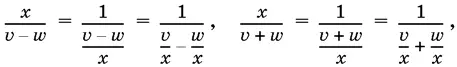
и обозначить v / x = у , w / x = z . Мы придем к системе относительно у и z , решив которую, вычислим 1/ y + z .

Однако такую систему можно было получить сразу, если бы мы не ввели в качестве неизвестного x пройденное пароходом расстояние.

В условии задачи не было чисел, выраженных в километрах, однако расстояние между пунктами являлось существенным связующим звеном. Это означает, что мы должны были принять его за единицу, а скорости v и w выражать в частях расстояния, пройденных за один час. В результате мы пришли бы к системе