Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

18.13.Пассажир, опоздавший на поезд, сначала решил догнать его на такси, однако через некоторое время пересел на автобус, заплатив за билет А p., и прибыл на одну из станций одновременно с поездом. Между тем он обнаружил, что если бы продолжал ехать на такси, то догнал бы поезд на τ ч раньше, истратив при этом на В p. меньше. Какова скорость поезда, если скорость такси v 1км/ч, автобуса v 2км/ч ( v 1> v 2), а стоимость проезда 1 км на такси а p.?

18.14.Товарный поезд, шедший из А в В , прибыл в С одновременно с пассажирским, шедшим из В в А со скоростью в m раз большей, чем скорость товарного поезда. Оба состава простояли t ч в пункте С , затем продолжили путь, причем каждый увеличил скорость на 25%. Товарный поезд прибыл в В на t 1ч позже, а пассажирский в А на t 2ч позже, чем если бы они двигались без остановки с первоначальной скоростью. Насколько раньше товарный поезд вышел из А , чем пассажирский из В ?

18.15.Расстояние между пунктами А и В равно s км. Из пункта А в пункт В вылетел вертолет, а через t ч в том же направлении вылетел самолет. Самолет догнал вертолет в d км от А , долетел до В и сразу повернул обратно. В d км от В самолет встретил вертолет и вернулся в А позднее, чем вертолет прибыл в В . Насколько раньше вертолет прибыл в В , чем самолет вернулся в А ?

18.16.В озеро впадают две реки. Пароход выходит из порта M на первой реке и плывет вниз по течению, затем через озеро (на озере течение отсутствует) и по второй реке вверх по течению до порта N . Придя в N , пароход отправляется в обратный путь.

Известна собственная скорость парохода v и скорости течения рек: v 1и v 2. На путь от M до N , равный по длине s , и на обратный путь пароход тратит одинаковое время t . Какое расстояние пароход проходит по озеру?

18.17.Из пункта А в пункт В в 8 ч утра выходит скорый поезд. В этот же момент из В в А выходят пассажирский и курьерский поезда, причем скорость курьерского в два раза больше скорости пассажирского. Скорый поезд прибывает в В в 13 ч 50 мин того же дня, а встречает курьерский поезд не ранее 10 ч 30 мин утра. Когда пассажирский поезд прибудет в пункт А , если между моментами встреч скорого поезда с курьерским и скорого поезда с пассажирским проходит не менее часа?

18.18.Завод должен получить 1100 деталей. На базе имеются комплекты по 70, 40 и 25 деталей. Стоимость пересылки одного комплекта равна соответственно 20, 10 и 7 p. Какие комплекты и в каком количестве следует заводу заказать, чтобы расходы по пересылке были наименьшими? Переупаковка комплектов на базе не допускается.

Рассмотрим функцию натурального аргумента а n = f ( n ), где либо n = 1, 2, 3, ..., k , либо n = 1, 2, 3, ..., k , ... . Если при любых натуральных i и j , таких, что i < j , значение а j считается последующим по отношению к а i , то множество значений а n этой функции образует последовательность .

Последовательность обозначают, записывая ее члены а n один за другим в порядке возрастания номера n : а 1, a 2, а 3, ... .

Если номер n принимает значения n = 1, 2, 3, ..., k , то последовательность называется конечной. Если же n = 1, 2, 3, ... (т. е. n пробегает все натуральные числа), то последовательность называется бесконечной.

а n = f ( n ) называется общим членом последовательности. Если для любых i и j , таких, что i < j , выполняется неравенство а i < а j , то последовательность называется возрастающей. Если при тех же условиях будет а i > а j , то последовательность называется убывающей. Если же при любых i и j , таких, что i < j , выполняется неравенство а i ≤ а j ( а i ≥ а j ), то последовательность называется неубывающей ( невозрастающей ).

Последовательность, в которой

а i + 1= а i + d

при всех натуральных i , называется арифметической прогрессией. Число d называется разностью арифметической прогрессии. Имеют место формулы:

2 а n = а n + 1+ а n − 1; а n = а 1+ d ( n − 1);

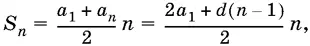
где S n — сумма n первых членов прогрессии.

Последовательность, в которой

a i + 1= qa i

при всех натуральных i , причем q ≠ 0 и a i ≠ 0, называется геометрической прогрессией , а число q называется ее знаменателем .

Для геометрической прогрессии имеют место формулы:

a n = a 1 q n − 1; 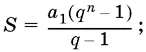a ² n = a n − 1 a n + 1.

Вторая формула верна, если q ≠ 1. Бесконечная геометрическая прогрессия, у которой | q | < 1, называется бесконечно убывающей .

Бесконечно убывающая геометрическая прогрессия не обязательно является убывающей последовательностью. Она может быть возрастающей, например, при a 1= −1, q = ½ , а может быть колеблющейся: a 1= 1, q = −½ .

Если для бесконечной последовательности существует конечный предел последовательности ее сумм S n , т. е. существует 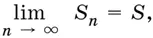, то S называется суммой всех членов этой бесконечной последовательности.

Для того чтобы бесконечная геометрическая прогрессия имела сумму всех своих членов, необходимо и достаточно, чтобы она была бесконечно убывающей. В этом случае

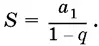
19.1.Общий член последовательности 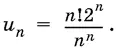Является эта последовательность возрастающей или убывающей?

19.2.Докажите, что если члены a p, a q, a r, a s арифметической прогрессии образуют геометрическую прогрессию, то последовательность p − q , q − r , r − s является геометрической прогрессией.

19.3.Докажите, что если положительные числа a , b , с — соответственно m -й, n -й и p -й члены как арифметической, так и геометрической прогрессии, то