Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

21.8.Найдите число неподобных между собой членов разложения

(а + b + с + d ) n .

21.9.Найдите коэффициент при х k в разложении

(1 + x + x ² + ... + х n − 1)².

21.10.Для бинома ( 1/ 5 x + 2/ 5) n найдите натуральный показатель n , если известно, что десятый член разложения этого бинома имеет наибольший коэффициент.

21.11.Определите число отличных от нуля коэффициентов в разложении

(1 + x ² + х 5) 20= а 0+ а 1 х + а 2 х ² + ... + а 100 х 100.

21.12.Дана последовательность а 1, а 2, а 3, ..., а 10. Сколькими способами, сохраняя фиксированный порядок элементов последовательности, ее можно разбить на группы, каждая из которых состоит из одного элемента или двух рядом стоящих элементов?

21.13.На плоскости проведены m параллельных прямых и n прямых, пересекающих эти прямые и друг друга. Никакие три прямые не проходят через одну точку. На сколько областей (частей) эти прямые разбивают плоскость?

Определения обратных тригонометрических функций приводят к следующим соотношениям.

Если arcsin x = α (−1 ≤ x ≤ 1), то sin α = x и − π/ 2≤ α ≤ π/ 2.

Если x ≥ 0, то 0 ≤ α ≤ π/ 2; если x ≤ 0, то − π/ 2 ≤ α ≤ 0.

Если arccos x = α (−1 ≤ x ≤ 1), то cos α = x и 0 ≤ α ≤ π.

Если x ≥ 0, то 0 ≤ α ≤ π/ 2; если x ≤ 0, то π/ 2 ≤ α ≤ π.

Если arctg x = α, то tg α = x и − π/ 2< α < π/ 2.

Если x ≥ 0, то 0 ≤ α < π/ 2; если x ≤ 0, то − π/ 2< α ≤ 0.

Если arctg x = α, то ctg α = x и 0 < α < π.

Если x ≥ 0, то 0 < α ≤ π/ 2; если x ≤ 0, то π/ 2 ≤ α < π.

Имеют место следующие соотношения [14] Первое соотношение — неабсолютное тождество, остальные — абсолютные тождества. :

arcsin x + arccos x = π/ 2; arctg x + arcctg x = π/ 2;

arcsin (− x ) = −arcsin x ; arctg (− x ) = −arctg x ; arccos (− x ) = π − arccos x ; arcctg (− x ) = π − arcctg x .

22.1.Докажите, что

2 arctg ¼ + arctg 7/ 23= π/ 4.

22.2.Представьте выражение

arctg 7/ 9+ arcctg 8 + arcsin √2/ 4

в виде значения функции arcsin x .

22.3.Представьте выражение

arctg (−2) + arcsin ⅓ + arctg (−⅓)

в виде значения лишь одной обратной тригонометрической функции.

22.4.Вычислите сумму

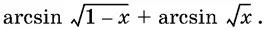
22.5.Найдите

arccos (sin π( x ² + x − З)),

если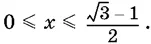

22.6.Докажите, что если 0 ≤ x ≤ 1, то

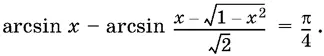
22.7.Докажите, что выражение arcsin 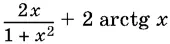не зависит от x , если x < −1, и упростите его в этом случае.

Решите уравнения:

22.8.tg (З arcsin x ) = 1.

22.9.arcsin 3 x / 5 + arcsin 4 x / 5 = arcsin x .

22.10.arcsin 2 x + arcsin x = π/ 3.

22.11.arctg (2 + cos x ) − arctg (2 cos² x / 2) = π/ 4.

22.12.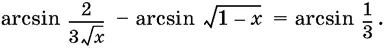

22.13.arctg ( x − 1) + arctg x + arctg ( x + 1) = arctg З x .

Областью определения функции может быть вся числовая ось ( у = x ², у = sin x ), луч с принадлежащей ему граничной точкой ( у = √ x , граничная точка x = 0 принадлежит области определения x ≥ 0) и с не принадлежащей ему граничной точкой ( у = lg x ), совокупность интервалов (замкнутых, открытых, полуоткрытых) и отдельных точек.

Важной характеристикой функции является ее периодичность. С помощью периодических функций можно описать явления, повторяющиеся через равные промежутки времени. Функция f ( x ) называется периодической, если существует такое число T ≠ 0, что для любого значения аргумента x ч и ́сла x + T и x − T также являются значениями аргумента и выполняется равенство f ( x + T ) = f ( x ).

Если T — период f ( x ) и x — значение аргумента, то x + nТ , где n — целое число, — также значение ее аргумента, а пТ — период функции f ( x ). В частности, если T — период, то и − T — тоже период.

Наименьший положительный период называется основным периодом.

23.1.Найдите область определения функции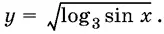

23.2.Найдите область определения функции

log 3log ½( x ² − x − 1).

23.3.При каких значениях x выражение 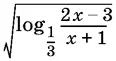принимает действительные значения?

23.4.Найдите область определения функции

arccos ( x ² − 3 х + 1) + tg 2 х .

23.5.Где расположены точки плоскости, для координат которых выражение

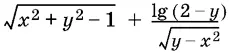
принимает действительные значения ?

23.6.Докажите, что функция у = cos x ² не является периодической.

23.7.Докажите, что если функция

f ( x ) = sin x + cos аx

периодическая, то а — рациональное число.

23.8.Найдите основной период функции

у = cos 3 x / 2− sin x / 3.

24.1. Найдите все значения x, при которых функция

sin x − cos² x − 1

принимает наименьшее значение.

24.2. Найдите наибольшее значение функции

у = sin 2 х sin (2 х − π/ 6).

При каких значениях x оно достигается?

24.3. Найдите наибольшее значение функции

у = sin x cos² x − sin³ x cos x .

24.4. При каких значениях x и у выражение

2 х ² + 2 ху + у ² − 2 х + 2 у + 2

имеет наименьшее значение. Найдите это наименьшее значение.

24.5. Найдите наименьшее значение выражения

у = | х ² − 1| + | х ² − 4| + | x + 2| + | x + 1|.

24.6. Найдите наименьшее значение функции

у = х 7+ a / 7 x , где x > 0, а > 0.

24.7. В круг радиусом R вписывается данный угол α. Какими должны быть длины хорд, образующих этот угол, чтобы их сумма была наибольшей?