Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
24.8.В основании прямой призмы лежит прямоугольный треугольник с площадью, равной 2 м², а высота призмы равна гипотенузе основания. Какими должны быть стороны основания, чтобы боковая поверхность призмы была наименьшей?
24.9.Найдите сторону наибольшего из квадратов, внутренние точки которых находятся внутри правильного шестиугольника со стороной а .
24.10.Найдите наибольшее значение дроби 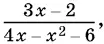 если x может принимать любые действительные значения.
если x может принимать любые действительные значения.
24.11.Контейнер для приборов должен быть сконструирован в форме прямоугольного параллелепипеда объемом 7,2 м³, причем площадь полной поверхности контейнера не должна превышать 24 м² при условии, что периметр основания не станет менее 10 м. Найдите размеры такого контейнера.
24.12.Найдите наименьшее значение функции
у = ctg² (α − x ) + ctg² (α + x ), 0 < α < π/ 2.
24.13.Найдите наибольшее и наименьшее значения функции
arcsin³ x + arccos³ x .
24.14.Найдите наименьшее значение функции
у = 2 sin² x − 3 sin 2 x + 10 cos² x .
24.15.Найдите наименьшее значение суммы у + w , если x , у , z , w удовлетворяют системе
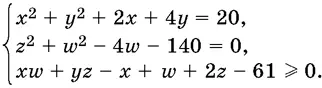
Указания
Первые указания
K главе 1
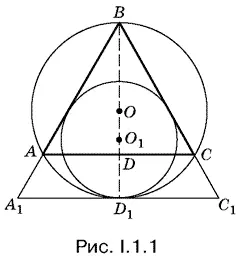
1.1.Если через точку D 1касания окружностей провести их общую касательную, то, пересекая продолжения сторон ВА 1и ВС 1, она образует треугольник А 1 ВС 1(рис. I.1.1). Воспользуйтесь тем, что OD = DD 1= R / 2, а O 1 D 1= BD 1 / 3.
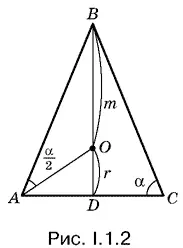
1.2.В треугольнике АОВ ( O — центр вписанной окружности, рис. I.1.2) угол ВАО равен α/ 2, а угол ВОА равен сумме углов OAD и ODA , т. е. равен π/ 2 + α/ 2. По условию BO = m , так как BD = r + m . Поэтому решение удобно начать с определения AB из треугольника BOA .
1.3.Вначале нужно выяснить смысл выражения «окружность делит сторону треугольника пополам». Если окружность имеет со стороной треугольника две общие точки, то ни про одну мы не сможем сказать, что она делит отрезок пополам, поскольку отрезок разделится на три части.
1.4.Отношение площади треугольника А 1 В 1 С 1к площади треугольника АВС (рис. I.1.4) можно записать так:
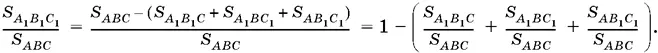
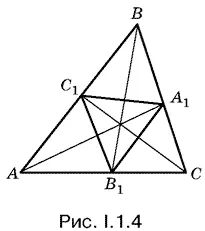
Теперь нужно найти каждое из отношений, входящих в правую часть.
1.5.Углы определяют треугольник лишь с точностью до подобия. Если ввести в рассмотрение один линейный элемент и выразить через него обе площади, то при подсчете отношения площадей этот элемент сократится. В качестве такого линейного элемента удобно выбрать радиус r вписанной в треугольник окружности.
1.6.Так как В = 3 C (рис. I.1.6), то сторона AB меньше стороны AC и можно доказать, что площадь треугольника АВD ( АD — биссектриса треугольника АВС ) меньше площади треугольника ADC . Таким образом по условию 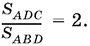
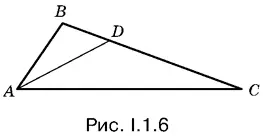
1.7.Применить метод сравнения площадей.
1.8.Все участвующие в задаче величины связаны с площадью треугольника, которая известна. Воспользоваться сравнением площадей.
1.9.В треугольнике даны две биссектрисы и отношение, в котором эти биссектрисы делятся точкой их пересечения. Наряду с данными отношениями естественно воспользоваться свойством отрезков, на которые биссектриса делит противоположную сторону треугольника. Поскольку требуется определить углы треугольника, то от отношений данных линейных величин нужно перейти к отношению сторон данного треугольника.
1.10.Продолжить отрезок QМ до пересечения в точке А с другой стороной угла.
1.11.Известные высоты треугольника естественно связать между собой с помощью его площади. При этом вместо сторон треугольника удобнее рассматривать его углы, выразив стороны через третью высоту.
1.12.В соотношении b + с = k выразить b и с через известную высоту h и тригонометрические функции углов В и С .
1.13. Способ 1.Чтобы решить задачу, нужно установить связь между углом α, сторонами треугольника и его площадью. Однако установить эту связь непосредственно не удается. Поэтому необходимо рассматривать вспомогательные элементы, например перпендикуляры длины x , у и z , опущенные из точки О на стороны а , b , с соответственно.
Способ 2.Чтобы установить связь между углом α, сторонами треугольника и его площадью, можно ввести в рассмотрение длины отрезков: ОА = I , ОВ = m , ОС = n .
1.14.По условию CD = BC − AC ( D — основание высоты). Однако BC и AC можно выразить через CD с помощью тригонометрических функций углов треугольника АВС . Это даст нам уравнение, связывающее углы треугольника АВС .
1.15.Если рассматривать длины сторон AC = b и BC = а, то все участвующие в задаче геометрические величины будут связаны с площадью треугольника ABC.
1.16.Чтобы геометрически связать окружность с центром О и окружность с центром О 1, нужно провести отрезки СО и ВО (рис. I.1.16). Окружность О 1описана около треугольника СОВ. Длина хорды СВ известна. Следовательно, для того, чтобы найти радиус, достаточно определить угол СОВ.

1.17.Задачу удобно переформулировать иначе: через центр вписанной окружности проведем прямую, параллельную средней стороне треугольника, и докажем, что она пройдет через точку пересечения медиан, т. е. точка пересечения этой прямой с медианой, опущенной на меньшую сторону, делит медиану в отношении 2 : 1.
Читать дальшеИнтервал:
Закладка:










