Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
15.6.sin |lg x | + cos |lg x | > − 1/ √2.
15.7. 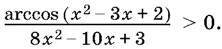
15.8.arctg √ x > arccos (1 − x ).
15.9.(4 х − x ² − 3) log 2(cos² π х + 1) ≥ 1.
15.10. 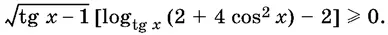
Глава 16
Трансцендентные уравнения
16.1.Докажите, что уравнение
2 sin² x / 2sin² x / 6= 1/ x ²+ x ²
не имеет корней.
Решите уравнения:
16.2. 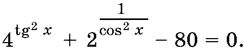
16.3.(tg x ) sin x = (ctg x ) cos x .
16.4.sin (2 х − 1+ 2 х − 2) cos (2 х − 1+ 2 х − 2) = ¼.
16.5.lg sin x + lg sin 5 х = lg sec 4 х .
16.6.lg² (sin x + 4) + 2 lg (sin x + 4) − 5/ 4= 0.
16.7.log sin x (sin x − ¼ cos x ) = 3.
16.8.log 8 cos² x sin x = ½.
16.9.Найдите положительные решения уравнения
tg [ 5π(½) x ] = 1.
16.10.Решите уравнение
lg² cos x + 2 lg cos x + m ² + 2 m − 3 = 0.
16.11.Для каждого действительного числа а решите уравнение
lg² sin x − 2 а lg sin x − а ² + 2 = 0.
16.12.Решите систему уравнений
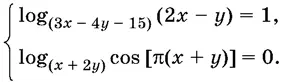
16.13.Решите уравнение
4 sin² π x + 4 cos² π x = −8 x ² + 12| x | − ½.
16.14.Решите уравнение
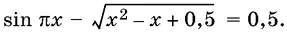
Глава 17
Функции и их свойства
17.1.Решите неравенство
4 f ( x ) + g ( x ) ≤ 0,
если функции f ( x ) и g ( x ) удовлетворяют системе
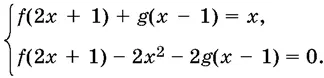
17.2.Сколько различных действительных корней имеет уравнение f ( f ( x )) = 0, где f ( x ) = x ³ − 6 x ² + 9 x ?
17.3.Найдите все целые x и у , удовлетворяющие системе
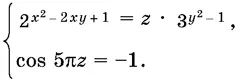
17.4.Решите систему уравнений
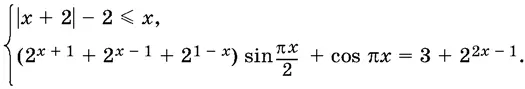
17.5.Дана функция f ( x ) = 6 х ² + 2 х + 6. Известно, что ее график касается графика первообразной F ( x ) этой функции в точке, абсцисса которой превосходит число 0,7. Найдите все значения x , для которых
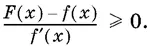
17.6.Изобразите на плоскости ( x , у ) множество точек, координаты которых удовлетворяют неравенству
log ( x − у )( x + у ) ≥ 1.
17.7.Найдите площадь фигуры, координаты точек которой удовлетворяют системе неравенств
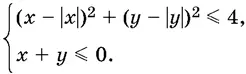
17.8.На координатной плоскости заданы точки A (0; 2), B (1; 7), С (10; 7) и D (7; 1). Найдите площадь пятиугольника ABCDE, где E — точка пересечения прямых AC и BD.
17.9.Фигура задана на координатной плоскости системой
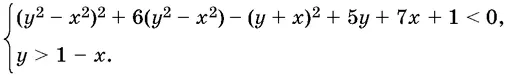
Сколько интервалов на прямой у = 2 − x образует ортогональная проекция данной фигуры на эту прямую?
17.10.При каких значениях параметра а уравнение
x ² − ( а + 3) x + 2 а + 7 = 0
имеет 2 различных целых корня?
17.11.В зависимости от а определите число действительных корней уравнения
х 4− (1 − 2 а ) x ² + а ² − 1 = 0.
17.12.При каких значениях параметра а уравнение
2(2 а − 1) sin 4 х − ( а + 3) cos 8 х + 3 а = 1
имеет ровно восемь решений на отрезке [−π, π]?
17.13.На плоскости ( x , у ) укажите все точки, через которые не проходит ни одна из кривых семейства
у = x ² + 2( а − 1) x + 2( а − 1)² − 1,
где а — действительное число.
Глава 18
Задачи на составление уравнений
При решении задач на составление уравнений основную трудность представляет перевод условия задачи с обычного языка на язык математических символов и уравнений. Наиболее ответственный этап этого процесса — выбор неизвестных. Нельзя шаблонно выбирать в качестве неизвестных величины, стоящие в вопросе задачи. Основное требование, которому должны отвечать выбранные неизвестные, состоит в том, чтобы с их помощью можно было прозрачно записать сформулированные в условии задачи соотношения.
Разберем в качестве примера следующую задачу.
Пример 1.Трое рабочих должны изготовить некоторое число деталей. Сначала к работе приступил первый, а через некоторое
время к нему присоединился второй. Когда 1/ 6работы была выполнена, к работе приступил третий. Работу они закончили одновременно. Сколько времени работал первый рабочий, если каждый изготовил одинаковое число деталей, причем третий работал на 2 ч меньше второго? Известно, что первый и второй, работая вместе, могут изготовить требуемое число деталей на 9 ч раньше, чем третий, если бы он работал один.
Известно, что каждый рабочий изготовил одинаковое число деталей, т. е. выполнил треть всей работы. С другой стороны, нет никаких сведений о числе деталей, изготовленных кем-либо в какой-либо промежуток времени. Это означает, что речь идет о работе «вообще», о том, что каждый выполнял какую-то часть этой работы, а потому всю работу следует принять за единицу. Ту же мысль подтверждает и условие, в силу которого третий рабочий приступил к работе, когда 1/ 6работы (обратите внимание: 1/ 6всей работы, а не 45 или 27 деталей) была уже выполнена.
Из условия следует, что рабочие работают по-разному, другими словами, они изготовляют разное число деталей за одно и то же время. Поэтому нужно ввести в рассмотрение производительность каждого из них. Однако через x , у и z мы обозначим не число деталей, изготовляемых в час первым, вторым и третьим рабочими соответственно, а ту часть всей работы, которую каждый из них выполняет за это время.
После всего сказанного должно быть очевидным, что мы легко перепишем условие задачи в виде системы уравнений, если введем в рассмотрение еще три неизвестные: t 1, t 2, t 3— время, затраченное соответственно первым, вторым и третьим рабочими. Так как каждый из них сделал за это время треть всей работы, то
Читать дальшеИнтервал:
Закладка:










