Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Поэтому целесообразно помнить решения уравнений:

sin x = 0, x = n π; sin x = 1, x = π/ 2+ 2 n π; sin x = −1, x = − π/ 2+ 2 n π;

cos x = 0, x = π/ 2+ n π; cos x = 1, x = 2 n π; cos x = −1, x = (2 n + 1)π;

tg x = 0, x = n π; ctg x = 0, x = π/ 2+ n π.

При решении уравнений удобно пользоваться теоремами: уравнение cos x = cos у равносильно совокупности уравнений x + у = 2 k π, x − у = 2 l π; уравнение sin x = sin у равносильно совокупности уравнений x + у = (2 k + 1)π, x − у = 2 l π. Обратите внимание на то обстоятельство, что в разных уравнениях, входящих в совокупность, вообще говоря, используют разные буквы для обозначения произвольного целого числа. Это следует из того, что уравнения для x + у и для x − у решаются независимо одно от другого. Переход от уравнения tg x = tg у к уравнению x − у = π k может привести к приобретению посторонних решений, если tg x и tg у перестают существовать.

Однородные уравнения.Уравнение вида

а 0sin k x + а 1sin k − 1 x cos x + ...

... + а k − 1 sin x cos k − 1 x + а k cos k x = 0 (1)

называется однородным , так как все слагаемые его левой части имеют одинаковую степень относительно sin x и cos x .

При α 0≠ 0 среди решений уравнения (1) не содержится значений x , при которых cos x = 0. В самом деле, полагая cos x = 0, мы получаем из уравнения (1): а 0sin k x = 0, откуда sin k x = 0, так как а 0≠ 0 по условию. Но это невозможно, поскольку нет таких значений x , при которых sin x и cos x одновременно обращаются в нуль.

Аналогично при а к ≠ 0 среди решений уравнения (1) не содержится значений x , при которых sin x = 0.

Наметим пути решения уравнения (1). Рассмотрим два случая.

Случай 1. a 0≠ 0 и а k ≠ 0. В этом случае, разделив уравнение (1) на cos k x , мы получим (поскольку cos x ≠ 0) равносильное ему алгебраическое уравнение

а 0 у к + а 1 у k − 1+ ... + а k − 1 у + а k = 0 (2)

относительно у = tg x .

Можно также делить уравнение (1) на sin k x . Тогда (поскольку sin x ≠ 0) мы получим равносильное уравнению (1) алгебраическое уравнение

а 0+ а 1 z + ... + а k − 1 z k − 1+ а kz k = 0 (3)

относительно z = ctg x .

Пример 1.Решить уравнение

sin³ x − 2 sin² x cos x − sin x cos² x + 2 cos³ x = 0. (4)

Разделив его на cos³ x , получим алгебраическое уравнение

у ³ − 2 у ² − у + 2 = 0,

где у = tg x . Последнее уравнение легко решается путем разложения его левой части на множители, и мы находим корни:

у 1= −1, у 2= 1, у 3= 2.

Теперь остается решить совокупность уравнений

tg x = −1, tg x = 1, tg x = 2.

Мы получим следующие корни уравнения (1):

x = n π ± π/ 4, x = n π + arctg 2.

Случай 2. a 0= 0, или a k = 0, или а 0= a k = 0. Пусть, например, a 0= a k = 0, а a 1≠ 0 и a k − 1≠ 0. Тогда уравнение (1) примет вид

a 1sin k − 1 x cos x + a 2sin k − 2 x cos² x + ...

... + a k − 2sin² x cos k − 2 x + a k − 1sin x cos k − 1 x = 0. (5)

В левой части уравнения выносим за скобки все, что возможно (в случае уравнения (5) мы можем вынести за скобки произведение sin x cos x ). В результате получим уравнение

sin x cos x ( a 1sin k − 1 x + a 2sin k − 2 x cos x + ...

... + a k − 2sin x cos k − 2 x + a k − 1cos k − 1 x ) = 0,

распадающееся на совокупность уравнений

sin 2 х = 0,

a 1sin k − 1 x + a 2sin k − 2 x cos x + ...

... + a k − 2sin x cos k − 2 x + a k − 1cos k − 1 x = 0,

первое из которых решается просто (см. с. 77), а пути решения второго уравнения показаны в случае 1).

Пример 2.Решить уравнение

sin 4 x cos x − 2 sin³ x cos² x − sin² x cos³ x + 2 sin x cos 4 x = 0.

Левую часть уравнения разлагаем на множители:

sin x cos x (sin³ x − 2 sin² x cos x − sin x cos² x + 2 cos³ x ) = 0. Получаем совокупность уравнений

sin x = 0, cos x = 0,

sin³ x − 2 sin² x cos x − sin x cos² x + 2 cos³ x = 0.

Решения первых двух уравнений даны на с. 77. Третье уравнение подробно рассмотрено в примере 1.

Системы тригонометрических уравнений.Предположим, что, преобразовывая систему тригонометрических уравнений, мы пришли к системе

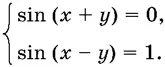
Если переписать эту систему в виде

то, складывая и вычитая полученные уравнения, придем к выводу, что

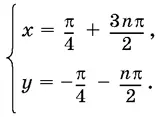
Решили ли мы систему? Оказывается, нет. Решить систему — значит, найти все ее решения, а из поля нашего зрения выпало такое очевидное решение как x = 3π/ 2, у = π/ 4(ни при каком целом n из выражения π/ 4+ 3 n π/ 2нельзя получить 3π/ 4).

В чем же ошибка? Ошибка очень проста: переходя от первоначальной системы к выражениям относительно x + у и x − у , мы должны были сохранить их «независимость», которая присутствовала в исходной системе. Вместо этого мы «связали» их введением общего целочисленного переменного n .

Правильным было бы такое решение:

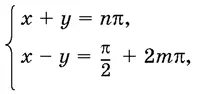
откуда

x = π/ 4+ (2 т + n ), у = − π/ 4− π/ 2(2 т − n ).

Прежде чем приступать к решению задач, ознакомьтесь с введением к главе 9.

Решите уравнения:

13.1.1 + sin 2 x + 2√2 cos 3 x sin ( x + π/ 4) = 2 sin x + 2 cos 3 x + cos 2 x .

13.2. .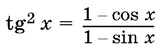

13.3. .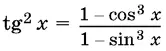

13.4.tg 2 x tg 7 x = 1.

13.5.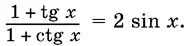

13.6.2 tg 3 x − 3 tg 2 x = tg² 2 x tg 3 x .

13.7.sin³ x + cos³ x + 1/ √2sin 2 x sin ( x + π/ 4) = cos x + sin 3 x .

13.8.4 tg 4 x − 4 tg 3 x − tg 2 x = tg 2 x tg 3 x tg 4 x .

13.9.Найдите решения уравнения

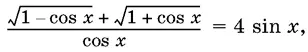
лежащие в интервале (0, 2π).