Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
11.27. 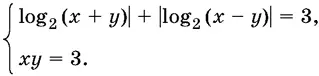
11.28. 
11.29. 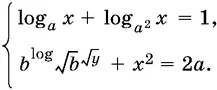
11.30. 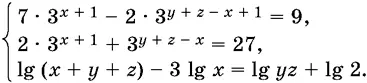
Глава 12
Тригонометрические преобразования
Основные тригонометрические формулы.
1. Зависимости между тригонометрическими функциями:
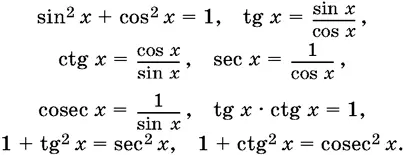
2. Тригонометрические функции суммы и разности аргументов:
sin ( x ± у ) = sin x cos у ± sin у cos x ,
cos ( x ± у ) = cos x cos у ± sin x sin у ,
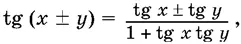
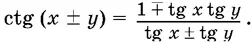
3. Функции двойного и тройного аргумента:

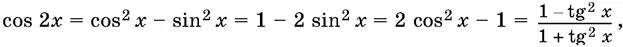
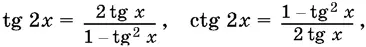
sin 3 х = 3 sin x − 4 sin³ x , cos 3 х = 4 cos³ x − 3 cos x .
4. Формулы понижения степени для синуса и косинуса:
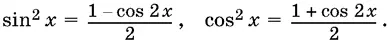
5. Функции половинного аргумента:
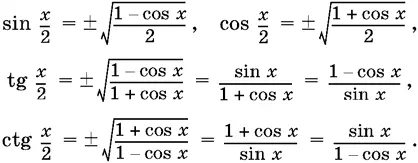
6. Преобразование суммы функций в произведение:
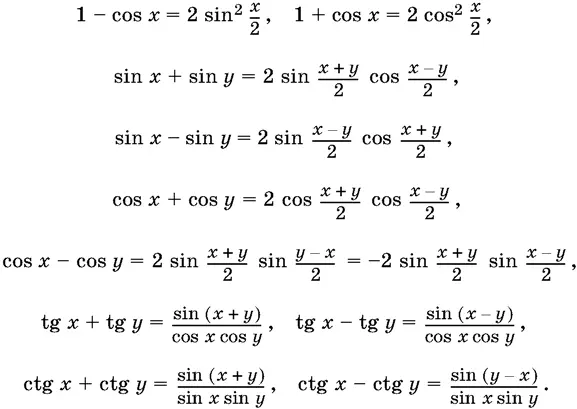
7. Преобразование произведения функций в сумму:
sin x cos y = ½[sin ( x − y ) + sin ( x + y )],
cos x cos y = ½[cos ( x − y ) + cos ( x + y )],
sin x sin y = ½[cos ( x − y ) − cos ( x + y )].
Все формулы нужно уметь читать не только «слева направо», но и «справа налево». Так, например, в записи sin π/ 4 cos x − cos π/ 4sin x нужно узнавать sin ( π/ 4− x ), а не принимать ошибочно за sin ( x − π/ 4), а в записи 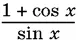 узнавать ctg x / 2.
узнавать ctg x / 2.
Проверьте себя и напишите, чему равно выражение  Если вы убеждены в том, что это выражение равно тангенсу половинного угла, обратите внимание на то обстоятельство, что выражение, о котором идет речь, неотрицательно, а тангенс половинного угла — знакопеременная функция. Таким образом,
Если вы убеждены в том, что это выражение равно тангенсу половинного угла, обратите внимание на то обстоятельство, что выражение, о котором идет речь, неотрицательно, а тангенс половинного угла — знакопеременная функция. Таким образом,
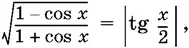
и не следует писать в этом случае ±tg x . То же самое рассуждение можно провести для любой из приведенных выше формул, где перед корнем стоит ±. Мы ставим ±, чтобы «примирить» выражение, стоящее в левой части, которое может быть отрицательным, с неотрицательным корнем. Поставив ±, мы не получаем двузначную функцию; этот символ говорит лишь о том, что для каждого фиксированного x мы обязаны выбрать определенный знак, в зависимости от того, в какой четверти тригонометрического круга оказывается угол, стоящий под знаком функции в левой части формулы.
12.1. Упростите выражение
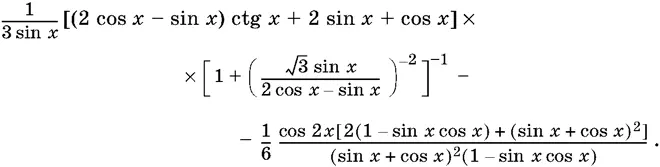
12.2. Докажите тождество
tg 2α tg (30° − α) + tg 2α tg (60° − α) + tg (60° − α) tg (30° − α) = 1.
12.3. Докажите тождество
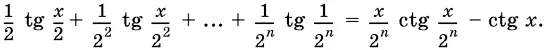
12.4. Докажите, что tg (α + β) = 2 tg α, если
sin α cos (α + β) = sin β и α + β ≠ π/ 2(2 n + 1), α ≠ π/ 2(2 n + 1), .
12.5. Вычислите без таблиц
cos π/ 7cos 2π/ 7cos 4π/ 7.
12.6. Вычислите без таблиц
tg π/ 7tg 2π/ 7tg 3π/ 7.
12.7. Докажите, что если  и
и 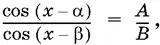 то при аВ + bA ≠ 0
то при аВ + bA ≠ 0 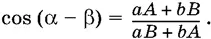
12.8. Докажите, что если |sin x | = | k sin у |, где −1 ≤ k ≤ 1, то произведение sin ( x + у ) sin ( x − у ) неположительно.
12.9. Докажите, что если sin α + sin β = а , cos α + cos β = b , то 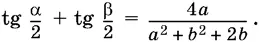
12.10. Дано
2 tg² α tg² β tg² γ + tg² α tg² β + tg² β tg² γ + tg² γ tg² α = 1.
Вычислите sin² α + sin² β + sin² γ.
12.11. Углы α, β, γ образуют арифметическую прогрессию с разностью π/ 3. Вычислите
А = tg α tg β + tg β tg γ + tg α tg γ.
12.12. Сумма трех положительных чисел α, β и γ равна π/ 2. Вычислите произведение ctg α ctg γ, если известно, что ctg α, ctg β и ctg γ образуют арифметическую прогрессию.
12.13. Вычислите без калькулятора и без таблиц
sin 106° + cos 106° ctg 8°.
Глава 13
Тригонометрические уравнения и системы
Простейшие тригонометрические уравнения.
sin x = а , x = n π + (−1) n arcsin а , | а | ≤ 1,
cos x = а , x = 2 n π ± arccos а , | а | ≤ 1,
tg x = а , x = n π + arctg а ,
ctg x = а , x = n π + arcctg а .
Во всех формулах n — произвольное целое число, т. е. n = 0; ±1; ±2; ±3; ... .
Решения уравнения sin x = а часто удобно записывать в виде двух серий корней:
x = 2 n π + αrсsin а , x = π(2 n + 1) − arcsin а .
Хотя приведенные формулы для решений уравнений sin x = а и cos x = а верны при всех значениях а, удовлетворяющих указанным справа ограничениям, при некоторых а эти формулы дают неудобный ответ.
Так, например, если к уравнению sin x = 1 применить общую формулу, то получим
x = n π + (−1) n π/ 2.
При n = 2 k получим x = 2 k π + π/ 2, а при n = 2 k + 1 получим x = 2 k π + π − π/ 2= 2 k π + π/ 2. При четном и нечетном n мы пришли к одинаковому ответу. Но этот же ответ можно получить гораздо проще, если не пользоваться общей формулой. Достаточно заметить, что sin x = 1 тогда и только тогда, когда подвижный радиус вертикален и направлен вверх.
Читать дальшеИнтервал:
Закладка:










